
【題目】某科研機構研發了某種高新科技產品,現已進入實驗階段.已知實驗的啟動資金為10萬元,從實驗的第一天起連續實驗,第![]() 天的實驗需投入實驗費用為
天的實驗需投入實驗費用為![]() 元
元![]() ,實驗30天共投入實驗費用17700元.
,實驗30天共投入實驗費用17700元.
(1)求![]() 的值及平均每天耗資最少時實驗的天數;
的值及平均每天耗資最少時實驗的天數;
(2)現有某知名企業對該項實驗進行贊助,實驗![]() 天共贊助
天共贊助![]() 元
元![]() .為了保證產品質量,至少需進行50天實驗,若要求在平均每天實際耗資最小時結束實驗,求
.為了保證產品質量,至少需進行50天實驗,若要求在平均每天實際耗資最小時結束實驗,求![]() 的取值范圍.(實際耗資=啟動資金+試驗費用-贊助費)
的取值范圍.(實際耗資=啟動資金+試驗費用-贊助費)
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
試題分析:(1)實驗開始后,每天的試驗費用構成公差為![]() ,首項為
,首項為![]() 的等差數列,通過等差數列的求和公式計算出這
的等差數列,通過等差數列的求和公式計算出這![]() 天所投入的試驗費用,然后便可求出
天所投入的試驗費用,然后便可求出![]() 的值,再利用等差數列的求和公式求出
的值,再利用等差數列的求和公式求出![]() 天內總計的試驗費用,然后再求出每天的平均試驗費用,利用基本不等式便可求出平均每天耗資最少時試驗的天數;(2)先求出實際耗資的連續函數,
天內總計的試驗費用,然后再求出每天的平均試驗費用,利用基本不等式便可求出平均每天耗資最少時試驗的天數;(2)先求出實際耗資的連續函數,![]() ,討論
,討論![]() 和
和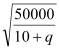 的大小關系即可解得
的大小關系即可解得![]() 的取值范圍為
的取值范圍為![]() .
.
試題解析:(1)依題意得,試驗開始后,每天的試驗費用構成等差數列,公差為![]() ,首項為
,首項為![]() ,
,
∴試驗30天共花費試驗費用為![]() ,
,
解得,![]() .............................2分
.............................2分
設試驗![]() 天,平均每天耗資為
天,平均每天耗資為![]() 元,則
元,則
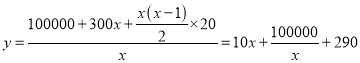 ..................4分
..................4分
![]() ,
,
當且僅當![]() ,即
,即![]() 時取等號,
時取等號,
綜上得,![]() ,試驗天數為100天..................................6分
,試驗天數為100天..................................6分
(2)設平均每天實際耗資為![]() 元,則
元,則
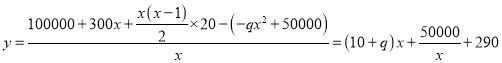 ...........8分
...........8分
當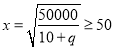 ,即
,即![]() 時,
時,
![]() ,因為
,因為![]() ,
,
所以,![]() ,.......................10分
,.......................10分
當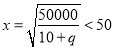 ,即
,即![]() 時,當
時,當![]() 時,
時,![]() 取最小值,
取最小值,
且![]() ,
,
綜上得,![]() 的取值范圍為
的取值范圍為![]() ....................12分
....................12分


科目:高中數學 來源: 題型:
【題目】已知數列{an}是公差為3的等差數列,數列{bn}是b1=1的等比數列,且![]() .
.
(Ⅰ)分別求數列{an},{bn}的通項公式;
(Ⅱ)令cn= an bn,求數列{cn}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,離心率為
,離心率為![]() ,點
,點![]() 為坐標原點,若橢圓
為坐標原點,若橢圓![]() 與曲線
與曲線![]() 的交點分別為
的交點分別為![]() (
(![]() 下
下![]() 上),且
上),且![]() 兩點滿足
兩點滿足![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過橢圓![]() 上異于其頂點的任一點
上異于其頂點的任一點![]() ,作
,作![]() 的兩條切線,切點分別為
的兩條切線,切點分別為![]() ,且直線
,且直線![]() 在
在![]() 軸、
軸、![]() 軸上的截距分別為
軸上的截距分別為![]() ,證明:
,證明:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了在冬季供暖時減少能量損耗,房屋的屋頂和外墻需要建造隔熱層,某幢建筑物要建造可使用20年的隔熱層,每厘米厚的隔熱層建造成本為6萬元,該建筑物每年的能源消耗費用![]() (單位:萬元)與隔熱層厚度
(單位:萬元)與隔熱層厚度![]() (單位:
(單位:![]() )滿足關系:
)滿足關系:![]() ,若不建隔熱層,每年能源消耗費用為8萬元,設
,若不建隔熱層,每年能源消耗費用為8萬元,設![]() 為隔熱層建造費用與20年的能源消耗費用之和.
為隔熱層建造費用與20年的能源消耗費用之和.
(1)求![]() 的值及
的值及![]() 的表達式;
的表達式;
(2)隔熱層修建多厚時,總費用![]() 達到最小,并求最小值.
達到最小,并求最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() ,
,![]() .
.![]() 是自然對數的底數.
是自然對數的底數.
(1)求曲線![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ,求實數
,求實數![]() ,
,![]() 的值;
的值;
(2)①若![]() 時,函數
時,函數![]() 既有極大值又有極小值,求實數
既有極大值又有極小值,求實數![]() 的取值范圍;
的取值范圍;
②若![]() ,
,![]() ,若
,若![]() 對一切正實數
對一切正實數![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍(用
的取值范圍(用![]() 表示).
表示).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點分別為
的兩個焦點分別為![]() ,
,![]() ,短軸的兩個端點分別為
,短軸的兩個端點分別為![]() ,
,![]() .
.
(1)若![]() 為等邊三角形,求橢圓
為等邊三角形,求橢圓![]() 的方程;
的方程;
(2)若橢圓![]() 的短軸長為2,過點
的短軸長為2,過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 、
、![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com