日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情

【題目】已知等差數列{an}的公差d≠0，且a1 ， a3 ， a13成等比數列，若a1=1，Sn是數列{an}前n項的和，則 （n∈N+）的最小值為（ ）
A.4
B.3
C.2 ﹣2
D.

【答案】A
【解析】解：∵a1=1，a1、a3、a13 成等比數列，
∴（1+2d）2=1+12d．
得d=2或d=0（舍去），
∴an =2n﹣1，
∴Sn= =n2 ，
∴ = ．
令t=n+1，則 =t+ ﹣2≥6﹣2=4
當且僅當t=3，即n=2時，∴ 的最小值為4．
故選：A．
【考點精析】本題主要考查了等差數列的性質的相關知識點，需要掌握在等差數列{an}中，從第2項起，每一項是它相鄰二項的等差中項；相隔等距離的項組成的數列是等差數列才能正確解答此題．

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

【題目】如圖，在三棱臺ABO﹣A1B1O1中，側面AOO1A1與側面OBB1O1是全等的直角梯形，且OO1⊥OB，OO1⊥OA，平面AOO1A1⊥平面OBB1O1 ， OB=3，O1B1=1，OO1= ．

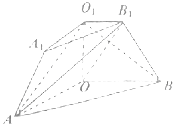
（1）證明：AB1⊥BO1；
（2）求直線AO1與平面AOB1所成的角的正切值；
（3）求二面角O﹣AB1﹣O1的余弦值．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】設函數f（x）=e|lnx|（e為自然對數的底數）．若x1≠x2且f（x1）=f（x2），則下列結論一定不成立的是（ ）
A.x2f（x1）＞1
B.x2f（x1）=1
C.x2f（x1）＜1
D.x2f（x1）＜x1f（x2）

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知函數f(x)=,下列結論中錯誤的是

A. , f()=0

B. 函數y=f(x)的圖像是中心對稱圖形

C. 若是f(x)的極小值點，則f(x)在區間（-∞,）單調遞減

D. 若是f（x）的極值點，則()=0

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】如圖，已知正方形ABCD和矩形ACEF所在的平面互相垂直，AB= ，AF=1，M是線段EF的中點．

（1）求證AM∥平面BDE；
（2）求二面角A﹣DF﹣B的大小；
（3）試在線段AC上一點P，使得PF與CD所成的角是60°．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】如圖，⊙O是以AB為直徑的圓，點C在圓上，在△ABC和△ACD中，∠ADC=90°，∠BAC=∠CAD，DC的延長線與AB的延長線交于點E．若EB=6，EC=6 ，則BC的長為 ．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知數列{an}的前n項和Sn=﹣an﹣（ ）n﹣1+2（n∈N*），數列{bn}滿足bn=2nan ．
（Ⅰ）求證數列{bn}是等差數列，并求數列{an}的通項公式；
（Ⅱ）設cn=log2 ，數列{ }的前n項和為Tn ， 求滿足Tn （n∈N*）的n的最大值．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知橢圓：（）的右焦點為，且橢圓上一點到其兩焦點，的距離之和為．

（1）求橢圓的標準方程；

（2）設直線：（）與橢圓交于不同兩點，，且，若點滿足，求的值．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知函數

（1）當時，求曲線在點處的切線方程；

（2）當時，討論的單調性.

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 国产精品99 | 91久久精品久久国产性色也91 | 久久精品久久久久电影 | 美日韩精品 | 国产高清在线精品 | 欧美黑人巨大xxx极品 | 国产一级视频在线播放 | 日韩av在线电影 | 国产精品美女久久久久图片 | 久久久久99 | 在线成人av| 色综合99 | 国产精品观看 | 综合婷婷| 日本一区二区免费看 | 息与子猛烈交尾一区二区 | 日韩精品一区二区三区四区 | 久久精品一区二区三区四区 | 欧美一级二级三级视频 | 日韩国产欧美一区二区 | 欧美成人免费在线观看 | 999精品视频 | 日日噜 | 国产91网址| 日韩久久一区二区 | 一区二区三区国产好 | 杏导航aⅴ福利网站 | 国产欧美一区二区三区国产幕精品 | 国产精品久久久久久久久久久久久 | 韩国精品一区 | 欧美成人高清视频 | 青娱乐精品视频 | 久久久精彩视频 | 91精品国产综合久久精品图片 | 久久久久网站 | 男人的午夜 | 中文字幕100页 | 久久久久久久久久国产 | 欧美三区视频 | 久久久久久久久久久久久国产精品 | 亚洲视频区 |