
設函數 的定義域為D,如果對于任意的
的定義域為D,如果對于任意的 ,存在唯一的
,存在唯一的 ,使
,使 (c為常數)成立,則稱函數
(c為常數)成立,則稱函數 在D上的均值為c.下列五個函數:①
在D上的均值為c.下列五個函數:①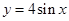 ②
② ③
③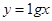 ④
④ ⑤
⑤ 滿足在其定義域上均值為2的所有函數的序號是 .
滿足在其定義域上均值為2的所有函數的序號是 .
②③⑤
解析試題分析:對于函數①y=4sinx,明顯不成立,因為y=4sinx是R上的周期函數,存在無窮個的x2∈D,使 成立.故不滿足條件;對于函數②y=x3,取任意的x1∈R,
成立.故不滿足條件;對于函數②y=x3,取任意的x1∈R,
 ,可以得到唯一的x2∈D.故滿足條件;對于函數③y=lgx,定義域為x>0,值域為R且單調,顯然必存在唯一的x2∈D,使
,可以得到唯一的x2∈D.故滿足條件;對于函數③y=lgx,定義域為x>0,值域為R且單調,顯然必存在唯一的x2∈D,使 成立.故成立;對于函數④y=2x定義域為R,值域為y>0.對于x1=3,f(x1)=8.要使
成立.故成立;對于函數④y=2x定義域為R,值域為y>0.對于x1=3,f(x1)=8.要使 成立,則f(x2)=-4,不成立;對于函數⑤y=2x-1定義域為任意實數,取任意的x1∈R,
成立,則f(x2)=-4,不成立;對于函數⑤y=2x-1定義域為任意實數,取任意的x1∈R,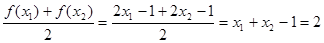 ,解得x2=3-x1,可以得到唯一的x2∈R.故成立,
,解得x2=3-x1,可以得到唯一的x2∈R.故成立,
故答案為:②③⑤.
考點:考查均值不等式在函數中的應用


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com