
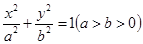 �����ҽ��c(di��n)�Ͷ��S��һ��(g��)���c(di��n)��(g��u)��߅�L�飴���������Σ�
�����ҽ��c(di��n)�Ͷ��S��һ��(g��)���c(di��n)��(g��u)��߅�L�飴���������Σ�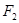 ��ֱ��
��ֱ�� �c�E�A���ཻ�ڣ������c(di��n)����
�c�E�A���ཻ�ڣ������c(di��n)����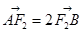 ����ֱ��
����ֱ��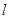 �ķ��̣�
�ķ��̣�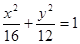 ����2��
����2��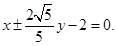
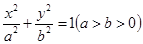 �����ҽ��c(di��n)�Ͷ��S��һ��(g��)���c(di��n)��(g��u)��߅�L�飴���������Σ����Կɵõ��ɂ�(g��)�P(gu��n)��
�����ҽ��c(di��n)�Ͷ��S��һ��(g��)���c(di��n)��(g��u)��߅�L�飴���������Σ����Կɵõ��ɂ�(g��)�P(gu��n)��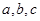 �ĵ�ʽ���Ķ����
�ĵ�ʽ���Ķ����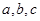 ����(y��ng)��ֵ.
����(y��ng)��ֵ.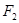 ��ֱ��
��ֱ��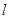 �c�E�A���ཻ�ڣ������c(di��n)����
�c�E�A���ཻ�ڣ������c(di��n)����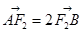 �������c(di��n)A,B�Ŀv����(bi��o)
�������c(di��n)A,B�Ŀv����(bi��o)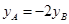 .����ͨ�^���O(sh��)ֱ������(li��n)���E�A���̼��ɵõ�һ��(g��)�P(gu��n)��x����y���Ķ��η��̣��ڽY(ji��)���f�_(d��)�����������k��ֵ������ýY(ji��)Փ.
.����ͨ�^���O(sh��)ֱ������(li��n)���E�A���̼��ɵõ�һ��(g��)�P(gu��n)��x����y���Ķ��η��̣��ڽY(ji��)���f�_(d��)�����������k��ֵ������ýY(ji��)Փ.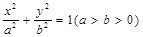 ��
��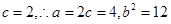 ,���ԙE�AC�ķ��̞�
,���ԙE�AC�ķ��̞�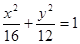 . 4��
. 4�� ������E�A���̵�(3
������E�A���̵�(3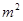 ��4)y2��12
��4)y2��12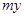 ��36��0.
��36��0.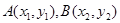 �����c(di��n)
�����c(di��n)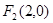 �t����(j��)
�t����(j��)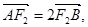 ����(2��
����(2��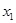 ����
����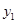 )��2(
)��2(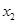 ��2��
��2��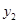 )��
)��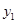 ��2
��2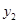 ��
�� ,����
,����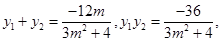
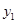 ��2
��2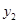 ��
��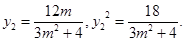
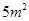 ��4����
��4����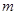 ��
��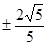 ������ֱ���ķ��̞�
������ֱ���ķ��̞�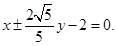 12��
12��

 ���n��(bi��o)�A����xӖ(x��n)��ϵ�д�
���n��(bi��o)�A����xӖ(x��n)��ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
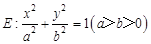 ��б�ʞ�1��ֱ������(j��ng)�^ԭ�c(di��n)
��б�ʞ�1��ֱ������(j��ng)�^ԭ�c(di��n)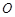 �������c�E�A�ཻ��
�������c�E�A�ཻ��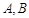 ���c(di��n)��
���c(di��n)��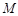 �龀��
�龀��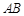 �����c(di��n).
�����c(di��n).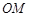 �c
�c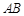 �ܷ�ֱ�����ܣ���
�ܷ�ֱ�����ܣ���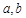 ֮�g�M����P(gu��n)ϵʽ�������ܣ��f�����ɣ�
֮�g�M����P(gu��n)ϵʽ�������ܣ��f�����ɣ�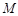 ��
��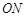 �����c(di��n)����
�����c(di��n)����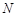 �c(di��n)�ڙE�A��.��
�c(di��n)�ڙE�A��.��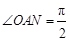 ����
����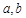 ֮�g�M����P(gu��n)ϵʽ.
֮�g�M����P(gu��n)ϵʽ.�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
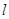 �c�E�A
�c�E�A
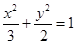 ����
����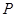
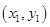 ��
��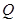
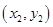 �ɲ�ͬ�c(di��n)���ҡ�
�ɲ�ͬ�c(di��n)���ҡ�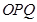 ����e
����e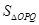 =
=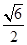 ������
������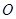 ������(bi��o)ԭ�c(di��n).
������(bi��o)ԭ�c(di��n).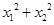 ��
��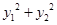 ���鶨ֵ��
���鶨ֵ��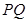 �����c(di��n)��
�����c(di��n)��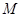 ����
����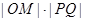 �����ֵ��
�����ֵ��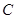 ���Ƿ�����c(di��n)
���Ƿ�����c(di��n)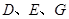 ��ʹ��
��ʹ��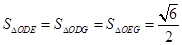 �������ڣ��Д��
�������ڣ��Д��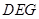 ���Π�������ڣ�Ո�f������.
���Π�������ڣ�Ո�f������.�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
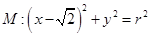
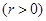 ,���E�A
,���E�A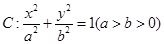 ������c(di��n)��A
������c(di��n)��A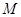 �ĈA�ģ��x���ʞ�
�ĈA�ģ��x���ʞ�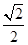 ��
�� ��ʹ��ֱ��
��ʹ��ֱ��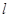 �c�E�A
�c�E�A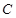 �քe����
�քe����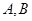 ���c(di��n)���c�A
���c(di��n)���c�A �քe����
�քe���� ���c(di��n)���c(di��n)
���c(di��n)���c(di��n)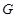 �ھ���
�ھ���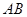 �ϣ���
�ϣ���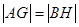 ����A
����A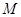 �İ돽
�İ돽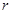 ��ȡֵ������
��ȡֵ�������鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
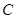 ��
��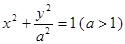 ���x���ʞ�
���x���ʞ� 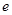 ���c(di��n)
���c(di��n)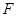 �����½��c(di��n)���c(di��n)
�����½��c(di��n)���c(di��n)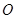 ������(bi��o)ԭ�c(di��n)���^
������(bi��o)ԭ�c(di��n)���^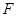 ��ֱ��
��ֱ�� 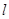 ��
��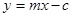 ������
������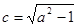 ���c�E�A
���c�E�A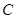 �ཻ��
�ཻ��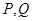 ���c(di��n)���ҝM�㣺
���c(di��n)���ҝM�㣺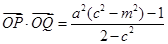 .
.
 ��ʾ
��ʾ 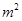 ��
��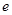 �����ֵ��
�����ֵ��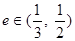 ����
���� 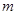 ��ȡֵ����.
��ȡֵ����.�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
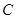 ���������(bi��o)ԭ�c(di��n)�����c(di��n)
���������(bi��o)ԭ�c(di��n)�����c(di��n)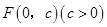 ��ֱ��
��ֱ��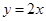 �ľ��x��
�ľ��x��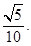
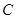 �ķ��̣�
�ķ��̣�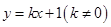 �c���タ
�c���タ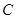 ����
����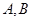 ���c(di��n)���O(sh��)����
���c(di��n)���O(sh��)����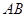 ������c
������c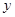 �S�����c(di��n)
�S�����c(di��n)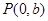 ����
����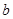 ��ȡֵ����.
��ȡֵ����.�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
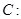
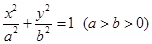 �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe�� ��
��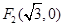 ���E�A�ϵ��c(di��n)
���E�A�ϵ��c(di��n)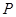 �M��
�M�� ����
����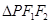 ����e
����e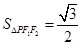 ��
��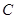 �ķ��̣�
�ķ��̣� ��ʹ
��ʹ �c�E�A
�c�E�A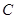 ���ڲ�ͬ�ă��c(di��n)
���ڲ�ͬ�ă��c(di��n)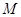 ��
��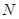 ���Ҿ���
���Ҿ���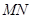 ǡ��ֱ��
ǡ��ֱ��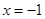 ƽ�֣������ڣ����
ƽ�֣������ڣ���� ��б��ȡֵ�������������ڣ�Ո�f�����ɣ�
��б��ȡֵ�������������ڣ�Ո�f�����ɣ��鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
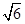 ���AO��x2��y2��5���E�AE��
���AO��x2��y2��5���E�AE��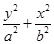 ��1(a>b>0)���x����e��
��1(a>b>0)���x����e��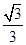 ��ֱ��l���AO�صõ����L�c�E�A�Ķ��S�L��ȣ�
��ֱ��l���AO�صõ����L�c�E�A�Ķ��S�L��ȣ��鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ����x�}
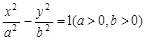 �����c(di��n)��F1��������c(di��n)�քe��A1��A2��P���p����������һ�c(di��n)���t�քe�Ծ���PF1��A1A2��ֱ���ăɂ�(g��)�A��λ���P(gu��n)ϵ�飨 ��
�����c(di��n)��F1��������c(di��n)�քe��A1��A2��P���p����������һ�c(di��n)���t�քe�Ծ���PF1��A1A2��ֱ���ăɂ�(g��)�A��λ���P(gu��n)ϵ�飨 ��| A���ཻ | B������ | C�����x | D��������r���п��� |
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com