已知盒子A中有m個紅球與10-m個白球,盒子B中有10-m個紅球與m個白球(兩個盒子中的球形狀、大小都相同).
(Ⅰ)分別從A、B中各取一個球,ξ表示紅球的個數.
(ⅰ)請寫出隨機變量ξ的分布規律,并證明Eξ等于定值;
(ⅱ)當Dξ取到最小值時,求m的值.
(Ⅱ)在盒子A中不放回地摸取3個球.事件A:在第一次取到紅球后,以后兩次都取到白球.事件B:在第一次取到白球后,以后兩次都取到紅球,若P(A)=P(B),求m的值.
【答案】
分析:(Ⅰ) 由題意可得:ξ表示紅球的個數,則ξ可能取的值為:0,1,2,
(i)根據題意分別求出ξ為0,1,2時的概率,即可得到其分布列進而得到其數學期望為定值.
(ii)由(i)并且結合方差的計算公式可得:
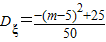
,并且1≤m≤9,再由二次函數的性質可得答案.
(Ⅱ)根據題意分別求出事件A與事件B方式的概率,利用其相等可得等式,進而求出m的數值.
解答:解:(Ⅰ) 由題意可得:ξ表示紅球的個數,則ξ可能取的值為:0,1,2,
(i)根據題意可得:P(ξ=0)=
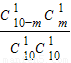
=
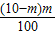
,P(ξ=1)=
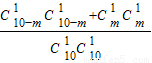
=
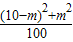
,P(ξ=2)=
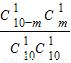
=

,
所以ξ的分布列為:
所以
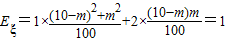
,
所以Eξ等于定值1.
(ii)由(i)可得:

,并且1≤m≤9,
所以當m=1=9時D
ξ取最小值為:

.
(Ⅱ)因為事件A:在第一次取到紅球后,以后兩次都取到白球,
所以
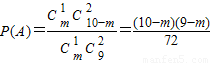
,
又因為事件B:在第一次取到白球后,以后兩次都取到紅球,
所以

.
因為P(A)=P(B),
所以
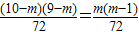
,解得:m=5.
點評:解決此類問題的關鍵是熟練掌握等可能事件與相互獨立事件的概率公式,以及離散型隨機變量的分布列與數學期望,此題由于含有參數因此在解答、計算與理解上都有一定的難度,學生在處理問題時要細心仔細并且正確分析問題即可得到全分,此題屬于難題.

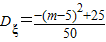 ,并且1≤m≤9,再由二次函數的性質可得答案.
,并且1≤m≤9,再由二次函數的性質可得答案.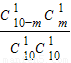 =
=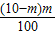 ,P(ξ=1)=
,P(ξ=1)=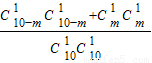 =
=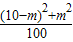 ,P(ξ=2)=
,P(ξ=2)=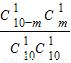 =
= ,
,
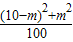
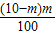
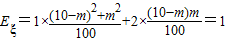 ,
, ,并且1≤m≤9,
,并且1≤m≤9, .
.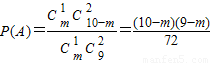 ,
, .
.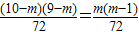 ,解得:m=5.
,解得:m=5.
