
【題目】如圖:橢圓![]() 與雙曲線
與雙曲線![]() 有相同的焦點
有相同的焦點![]() 、
、![]() ,它們在
,它們在![]() 軸右側(cè)有兩個交點
軸右側(cè)有兩個交點![]() 、
、![]() ,滿足
,滿足![]() .將直線
.將直線![]() 左側(cè)的橢圓部分(含
左側(cè)的橢圓部分(含![]() ,
, ![]() 兩點)記為曲線
兩點)記為曲線![]() ,直線
,直線![]() 右側(cè)的雙曲線部分(不含
右側(cè)的雙曲線部分(不含![]() ,
, ![]() 兩點)記為曲線
兩點)記為曲線![]() .以
.以![]() 為端點作一條射線,分別交
為端點作一條射線,分別交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() (點
(點![]() 在第一象限),設(shè)此時
在第一象限),設(shè)此時![]() .
.
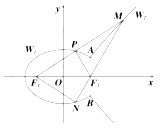
(1)求![]() 的方程;
的方程;
(2)證明: ![]() ,并探索直線
,并探索直線![]() 與
與![]() 斜率之間的關(guān)系;
斜率之間的關(guān)系;
(3)設(shè)直線![]() 交
交![]() 于點
于點![]() ,求
,求![]() 的面積
的面積![]() 的取值范圍.
的取值范圍.
【答案】(1)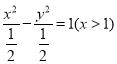 (2)見解析(3)
(2)見解析(3)![]()
【解析】試題分析:(1)根據(jù)橢圓方程求出右焦點![]() ,根據(jù)
,根據(jù)![]() 得到
得到![]() 、
、![]() 關(guān)于
關(guān)于![]() 軸對稱,所以求出
軸對稱,所以求出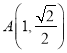 ,
, 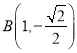 ,所以求出雙曲線的方程;(2)設(shè)
,所以求出雙曲線的方程;(2)設(shè)![]()
![]() ,得
,得![]() ,
, ![]() ,由
,由![]() ,得
,得![]() ,即
,即![]() ,又因為
,又因為![]()
![]() 分別在曲線
分別在曲線![]() 和
和![]() 上,有,
上,有,
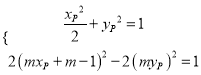 ,消去
,消去![]() ,得,
,得, ![]() (*),所以
(*),所以![]() 點坐標為
點坐標為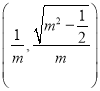 ,
, 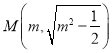 .所以直線
.所以直線![]() 的斜率
的斜率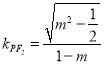 ,直線
,直線![]() 的斜率
的斜率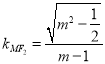 .所以
.所以![]() 與
與![]() 斜率之和為零;(3)由(2)知直線
斜率之和為零;(3)由(2)知直線![]() 與
與![]() 關(guān)于
關(guān)于![]() 軸對稱,結(jié)合橢圓的對稱性知點
軸對稱,結(jié)合橢圓的對稱性知點![]() 與點
與點![]() 關(guān)于
關(guān)于![]() 軸對稱,故
軸對稱,故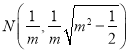 ,所以
,所以![]()
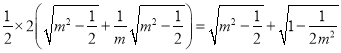 ,利用函數(shù)單調(diào)求出
,利用函數(shù)單調(diào)求出![]() 的范圍。
的范圍。
試題解析:(1)由條件,得![]() ,根據(jù)
,根據(jù)![]() 知,
知, ![]() 、
、![]() 、
、![]() 三點共線,
三點共線,
且由橢圓與雙曲線的對稱性知, ![]() 、
、![]() 關(guān)于
關(guān)于![]() 軸對稱,
軸對稱,
故![]() 所在直線為
所在直線為![]() ,從而得
,從而得 ,
, 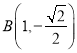 .
.
所以, ![]() ,又因為
,又因為![]() 為雙曲線的焦點,所以
為雙曲線的焦點,所以![]() ,
,
解得![]() .
.
因此, ![]() 的方程為
的方程為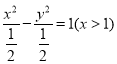 .
.
(2)由![]()
![]() ,得
,得![]() ,
, ![]() ,
,
由條件,得![]() ,即
,即![]() ,
,
由![]()
![]() 分別在曲線
分別在曲線![]() 和
和![]() 上,有,
上,有,
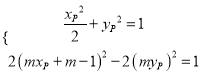 ,消去
,消去![]() ,得,
,得,
![]() (*),
(*),
將![]() 代入方程(*),成立,因此(*)有一根
代入方程(*),成立,因此(*)有一根![]() ,結(jié)合韋達定理得另一根為
,結(jié)合韋達定理得另一根為![]() ,因為
,因為![]() ,所以
,所以![]() ,舍去.
,舍去.
所以, ![]() .
.
從而![]() 點坐標為
點坐標為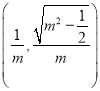 .
.
所以,直線![]() 的斜率
的斜率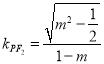 ,
,
由![]() ,得
,得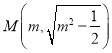 .
.
所以,直線![]() 的斜率
的斜率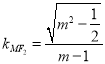 .
.
因此, ![]() 與
與![]() 斜率之和為零.
斜率之和為零.
(3)由(2)知直線![]() 與
與![]() 關(guān)于
關(guān)于![]() 軸對稱,結(jié)合橢圓的對稱性知點
軸對稱,結(jié)合橢圓的對稱性知點![]() 與點
與點![]() 關(guān)于
關(guān)于![]() 軸對稱,故
軸對稱,故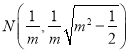 ,
,
因此, ![]()
 ,
,
![]() ,
,
因為![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
所以![]() 的取值范圍是
的取值范圍是![]() .
.


 期末寶典單元檢測分類復(fù)習(xí)卷系列答案
期末寶典單元檢測分類復(fù)習(xí)卷系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)f(x)=![]() (cosx﹣sinx)sin(x+
(cosx﹣sinx)sin(x+![]() )﹣2asinx+b(a>0).
)﹣2asinx+b(a>0).
(1)若b=1,且對任意![]() , 恒有f(x)>0,求a的取值范圍;
, 恒有f(x)>0,求a的取值范圍;
(2)若f(x)的最大值為1,最小值為﹣4,求實數(shù)a,b的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖1, 在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 為線段
為線段![]() 的中點. 將
的中點. 將![]() 沿
沿![]() 折起,使平面
折起,使平面![]()
![]() 平面
平面![]() ,得到幾何體
,得到幾何體![]() ,如圖2所示.
,如圖2所示.
(1)求證: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題滿分13分)已知函數(shù)![]() (
(![]() 為常數(shù),
為常數(shù),![]() )
)
(1)若![]() 是函數(shù)
是函數(shù)![]() 的一個極值點,求
的一個極值點,求![]() 的值;
的值;
(2)求證:當![]() 時,
時,![]() 在
在![]() 上是增函數(shù);
上是增函數(shù);
(3)若對任意的![]() ,總存在
,總存在![]() ,使不等式
,使不等式![]() 成立,求正實數(shù)
成立,求正實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】現(xiàn)有正整數(shù)構(gòu)成的數(shù)表如下:
第一行:1
第二行:1 2
第三行:1 1 2 3
第四行:1 1 2 1 1 2 3 4
第五行:1 1 2 1 1 2 3 1 1 2 1 1 2 3 4 5
…… …… ……
第![]() 行:先抄寫第1行,接著按原序抄寫第2行,然后按原序抄寫第3行,...,直至按原序抄寫第
行:先抄寫第1行,接著按原序抄寫第2行,然后按原序抄寫第3行,...,直至按原序抄寫第![]() 行,最后添上數(shù)
行,最后添上數(shù)![]() .(如第四行,先抄寫第一行的數(shù)1,接著按原序抄寫第二行的數(shù)1,2,接著按原序抄寫第三行的數(shù)1,1,2,3,最后添上數(shù)4).
.(如第四行,先抄寫第一行的數(shù)1,接著按原序抄寫第二行的數(shù)1,2,接著按原序抄寫第三行的數(shù)1,1,2,3,最后添上數(shù)4).
將按照上述方式寫下的第![]() 個數(shù)記作
個數(shù)記作![]() (如
(如![]() )
)
(1)用![]() 表示數(shù)表第
表示數(shù)表第![]() 行的數(shù)的個數(shù),求數(shù)列
行的數(shù)的個數(shù),求數(shù)列![]() 的前
的前![]() 項和
項和![]() ;
;
(2)第8行中的數(shù)是否超過73個?若是,用![]() 表示第8行中的第73個數(shù),試求
表示第8行中的第73個數(shù),試求![]() 和
和![]() 的值;若不是,請說明理由;
的值;若不是,請說明理由;
(3)令![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 的三個頂點為
的三個頂點為![]() ,
, ![]() 為
為![]() 的中點.求:
的中點.求:
(1) ![]() 所在直線的方程;
所在直線的方程;
(2) ![]() 邊上中線
邊上中線![]() 所在直線的方程;
所在直線的方程;
(3) ![]() 邊上的垂直平分線
邊上的垂直平分線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 在
在![]() 處的切線方程為
處的切線方程為![]()
(Ⅰ)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)若![]() 為整數(shù),當
為整數(shù),當![]() 時,
時, ![]() 恒成立,求
恒成立,求![]() 的最大值(其中
的最大值(其中![]() 為
為![]() 的導(dǎo)函數(shù)).
的導(dǎo)函數(shù)).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() ).
).
(Ⅰ)若函數(shù)![]() 在
在![]() 處的切線平行于直線
處的切線平行于直線![]() ,求實數(shù)
,求實數(shù)![]() 的值;
的值;
(Ⅱ)討論![]() 在
在![]() 上的單調(diào)性;
上的單調(diào)性;
(Ⅲ)若存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示的是一個幾何體的直觀圖和三視圖(其中正視圖為直角梯形,俯視圖為正方形,側(cè)視圖為直角三角形).
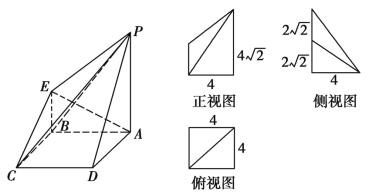
(1)求四棱錐P-ABCD的體積;
(2)若G為BC上的動點,求證:AE⊥PG.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com