
【題目】已知橢圓![]() 的兩焦點為
的兩焦點為![]() ,
,![]() ,且橢圓上一點
,且橢圓上一點![]() ,滿足
,滿足![]() ,直線
,直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點,與
兩點,與![]() 軸、
軸、![]() 軸分別交于點
軸分別交于點![]() 、
、![]() ,且
,且![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)當△![]() 面積取得最大值,且點
面積取得最大值,且點![]() 在橢圓
在橢圓![]() 上時,求
上時,求![]() 的值.
的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 與
與![]() 軸正半軸交于點
軸正半軸交于點![]() ,與
,與![]() 軸交于
軸交于![]() 、
、![]() 兩點.
兩點.
(1)求過![]() 、
、![]() 、
、![]() 三點的圓
三點的圓![]() 的方程;
的方程;
(2)若![]() 為坐標原點,直線
為坐標原點,直線![]() 與橢圓
與橢圓![]() 和(1)中的圓
和(1)中的圓![]() 分別相切于點
分別相切于點![]() 和點
和點![]() (
(![]() 、
、![]() 不重合),求直線
不重合),求直線![]() 與直線
與直線![]() 的斜率之積.
的斜率之積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)函數![]() ,討論
,討論![]() 的單調性;
的單調性;
(2)曲線![]() 在點
在點![]() 處的切線為
處的切線為![]() ,是否存在這樣的點
,是否存在這樣的點![]() 使得直線
使得直線![]() 與曲線
與曲線![]() 也相切,若存在,判斷滿足條件的點
也相切,若存在,判斷滿足條件的點![]() 的個數,若不存在,請說明理由.
的個數,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某基地蔬菜大棚采用無土栽培方式種植各類蔬菜.根據過去50周的資料顯示,該基地周光照量![]() (小時)都在30小時以上,其中不足50小時的有5周,不低于50小時且不超過70小時的有35周,超過70小時的有10周.根據統計,該基地的西紅柿增加量
(小時)都在30小時以上,其中不足50小時的有5周,不低于50小時且不超過70小時的有35周,超過70小時的有10周.根據統計,該基地的西紅柿增加量![]() (千克)與使用某種液體肥料的質量
(千克)與使用某種液體肥料的質量![]() (千克)之間的關系如圖所示.
(千克)之間的關系如圖所示.
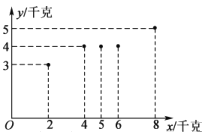
(1)依據上圖,是否可用線性回歸模型擬合![]() 與
與![]() 的關系?請計算相關系數
的關系?請計算相關系數![]() 并加以說明(精確到0.01).(若
并加以說明(精確到0.01).(若![]() ,則線性相關程度很高,可用線性回歸模型擬合)
,則線性相關程度很高,可用線性回歸模型擬合)
(2)蔬菜大棚對光照要求較大,某光照控制儀商家為該基地提供了部分光照控制儀,但每周光照控制儀運行臺數受周光照量![]() 限制,并有如下關系:
限制,并有如下關系:
周光照量 |
|
|
|
光照控制儀運行臺數 | 3 | 2 | 1 |
若某臺光照控制儀運行,則該臺光照控制儀周利潤為3000元;若某臺光照控制儀未運行,則該臺光照控制儀周虧損1000元.以頻率作為概率,商家欲使周總利潤的均值達到最大,應安裝光照控制儀多少臺?
附:相關系數公式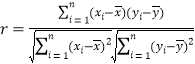 ,
,
參考數據:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某花圃為提高某品種花苗質量,開展技術創新活動,在![]() 實驗地分別用甲、乙方法培育該品種花苗.為觀測其生長情況,分別在實驗地隨機抽取各50株,對每株進行綜合評分,將每株所得的綜合評分制成如圖所示的頻率分布直方圖,記綜合評分為80分及以上的花苗為優質花苗.
實驗地分別用甲、乙方法培育該品種花苗.為觀測其生長情況,分別在實驗地隨機抽取各50株,對每株進行綜合評分,將每株所得的綜合評分制成如圖所示的頻率分布直方圖,記綜合評分為80分及以上的花苗為優質花苗.
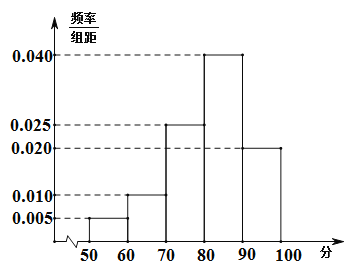
(1)用樣本估計總體,以頻率作為概率,若在![]() 兩塊實驗地隨機抽取3株花苗,求所抽取的花苗中優質花苗數的分布列和數學期望;
兩塊實驗地隨機抽取3株花苗,求所抽取的花苗中優質花苗數的分布列和數學期望;
(2)填寫下面的列聯表,并判斷是否有99%的把握認為優質花苗與培育方法有關.
優質花苗 | 非優質花苗 | 合計 | |
甲培育法 | 20 | ||
乙培育法 | 10 | ||
合計 |
附:下面的臨界值表僅供參考.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(參考公式: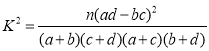 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠為生產一種精密管件研發了一臺生產該精密管件的車床,該精密管件有內外兩個口徑,監管部門規定“口徑誤差”的計算方式為:管件內外兩個口徑實際長分別為![]() ,標準長分別為
,標準長分別為![]() 則“口徑誤差”為
則“口徑誤差”為![]() 只要“口徑誤差”不超過
只要“口徑誤差”不超過![]() 就認為合格,已知這臺車床分晝夜兩個獨立批次生產.工廠質檢部在兩個批次生產的產品中分別隨機抽取40件作為樣本,經檢測其中晝批次的40個樣本中有4個不合格品,夜批次的40個樣本中有10個不合格品.
就認為合格,已知這臺車床分晝夜兩個獨立批次生產.工廠質檢部在兩個批次生產的產品中分別隨機抽取40件作為樣本,經檢測其中晝批次的40個樣本中有4個不合格品,夜批次的40個樣本中有10個不合格品.
(Ⅰ)以上述樣本的頻率作為概率,在晝夜兩個批次中分別抽取2件產品,求其中恰有1件不合格產品的概率;
(Ⅱ)若每批次各生產1000件,已知每件產品的成本為5元,每件合格品的利潤為10元;若對產品檢驗,則每件產品的檢驗費用為2.5元;若有不合格品進入用戶手中,則工廠要對用戶賠償,這時生產的每件不合格品工廠要損失25元.以上述樣本的頻率作為概率,以總利潤的期望值為決策依據,分析是否要對每個批次的所有產品作檢測?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com