
【題目】為考察高中生的性別與是否喜歡數學課程之間的關系,在某城市的某校高中生中,從男生中隨機抽取了70人,從女生中隨機抽取了50人,男生中喜歡數學課程的占![]() ,女生中喜歡數學課程的占
,女生中喜歡數學課程的占![]() ,得到如下列聯表.
,得到如下列聯表.
喜歡數學課程 | 不喜歡數學課程 | 合計 | |
男生 | |||
女生 | |||
合計 |
(1)請將列聯表補充完整;試判斷能否有90%的把握認為喜歡數學課程與否與性別有關;
(2)從不喜歡數學課程的學生中采用分層抽樣的方法,隨機抽取6人,現從6人中隨機抽取2人,求抽取的學生中至少有1名是女生的概率..
附:![]() ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】(1)見解析,沒有![]() 的把握(2)
的把握(2)![]()
【解析】試題分析:(1)將數據代入卡方公式求得![]() ,再對照參考數據得結論(2)先根據分層抽樣確定抽取男生女生人數,再利用枚舉法確定從6人中隨機抽取2人總事件數,從中確定至少有1名是女生事件數,最后根據古典概型概率公式求概率
,再對照參考數據得結論(2)先根據分層抽樣確定抽取男生女生人數,再利用枚舉法確定從6人中隨機抽取2人總事件數,從中確定至少有1名是女生事件數,最后根據古典概型概率公式求概率
試題解析:解:(Ⅰ)![]() 列聯表補充如下:
列聯表補充如下:
喜歡數學課程 | 不喜歡數學課程 | 合計 | |
男生 |
|
|
|
女生 |
|
|
|
合計 |
|
|
|
由題意得![]() ,
,
∵![]() ,∴沒有
,∴沒有![]() 的把握認為喜歡數學課程與否與性別有關.)
的把握認為喜歡數學課程與否與性別有關.)
(Ⅱ)用分層抽樣的方法抽取時,抽取比例是![]() ,
,
則抽取男生![]() 人,抽取女生
人,抽取女生![]() 人.
人.
記抽取的女生為![]() ,抽取的男生為
,抽取的男生為![]() ,
,
從中隨機抽取![]() 名學生共有
名學生共有![]() 種情況:
種情況:
![]()
![]() .
.
其中至少有![]() 名是女生的事件為:
名是女生的事件為:
![]() 有
有![]() 種情況.
種情況.
記“抽取的學生中至少有![]() 名是女生”為事件
名是女生”為事件![]() ,則
,則![]() .
.


 能力評價系列答案
能力評價系列答案 唐印文化課時測評系列答案
唐印文化課時測評系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sin ![]() +e﹣|x﹣1| , 有下列四個結論:
+e﹣|x﹣1| , 有下列四個結論:
①圖象關于直線x=1對稱;
②f(x)的最大值是2;
③f(x)的最大值是﹣1,;
④f(x)在區間[﹣2015,2015]上有2015個零點.
其中正確的結論是(寫出所有正確的結論序號).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在邊長為4的菱形![]() 中,
中, ![]() ,點
,點![]() 、
、![]() 分別在邊
分別在邊![]() 、
、![]() 上.點
上.點![]() 與點
與點![]() 、
、![]() 不重合,
不重合, ![]() ,
, ![]() ,沿
,沿![]() 將
將![]() 翻折到
翻折到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() .
.

(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)記三棱錐![]() 的體積為
的體積為![]() ,四棱錐
,四棱錐![]() 的體積為
的體積為![]() ,且
,且![]() ,求此時線段
,求此時線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 為圓
為圓![]() 上一動點,
上一動點,![]() 軸于點
軸于點![]() ,若動點
,若動點![]() 滿足
滿足![]() (其中
(其中![]() 為非零常數)
為非零常數)
(1)求動點![]() 的軌跡方程;
的軌跡方程;
(2)當![]() 時,得到動點
時,得到動點![]() 的軌跡為曲線
的軌跡為曲線![]() ,斜率為
,斜率為![]() 1的直線
1的直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點,求
兩點,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正項數列{an}滿足a1=1,(n+1)a2n+1+an+1an﹣na ![]() =0,數列{bn}的前n項和為Sn且Sn=1﹣bn .
=0,數列{bn}的前n項和為Sn且Sn=1﹣bn .
(1)求{an}和{bn}的通項;
(2)令cn= ![]() , ①求{cn}的前n項和Tn;
, ①求{cn}的前n項和Tn;
②是否存在正整數m滿足m>3,c2 , c3 , cm成等差數列?若存在,請求出m;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=cosx+ax2﹣1,a∈R.
(1)當a=0時,求函數f(x)在 ![]() 處的切線方程;
處的切線方程;
(2)當a=1時,求函數f(x)在[﹣π,π]上的最大值和最小值;
(3)若對于任意的實數x恒有f(x)≥0,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的三個內角A,B,C所對的邊分別為a,b,c,向量 ![]() =(c+a,b),
=(c+a,b), ![]() =(c﹣a,b﹣c),且
=(c﹣a,b﹣c),且 ![]() ⊥
⊥ ![]() .
.
(1)求角A的大小;
(2)若a=3,求△ABC周長的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知正方形ABCD的邊長為6,點E,F分別在邊AB,AD上,AE=AF=4,現將△AEF沿線段EF折起到△A′EF位置,使得A′C=2 ![]() .
. 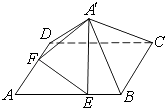
(1)求五棱錐A′﹣BCDFE的體積;
(2)求平面A′EF與平面A′BC的夾角.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com