已知函數y=x2-2ax+1(a為常數)在-2≤x≤1上的最小值為h(a),試將h(a)用a表示出來,并求出h(a)的最大值.
解:∵y=(x-a)
2+1-a
2,
∴拋物線y=x
2-2ax+1的對稱軸方程是x=a.(1分)
(1)當-2≤a≤1時,由圖①可知,當x=a時,該函數取最小值h(a)=1-a
2;(3分)
(2)當a<-2時,由圖②可知,當x=-2時,該函數取最小值h(a)=4a+5;(5分)
(3)當a>1時,由圖③可知,當x=1時,該函數取最小值h(a)=-2a+2(7分)
綜上,函數的最小值為
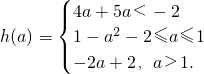
(8分)
當a<-2時h(a)<-3(9分)
當-2≤a≤1時-3≤h(a)≤1(10分)
當a>1時h(a)<0(11分)
∴h(a)≤1
∴h(a)
max=1(12分)
分析:由該函數的性質可知,該函數的最小值與拋物線的對稱軸的位置有關,于是需要對對稱軸的位置進行分類討論.
點評:解決二次函數的最值問題,應該先求出二次函數的對稱軸,判斷出對稱軸與區間的關系,進一步判斷出二次函數的單調性,進一步求出函數的最值.

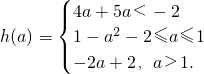 (8分)
(8分)
