【答案】
分析:這是一個幾何概型問題,關于x的方程x
2+2ax+b=0有實根根據判別式大于等于零,可以得到a和b之間的關系,寫出對應的集合,做出面積,得到概率.
解答:解:方程x
2+2ax+b=0有實根?△≥0?4a
2-4b≥0?b≤a
2,
(1)點(a,b)所構成的區域為Ω={(a,b)|-1≤a≤1,0≤b≤1},
面積S
Ω=2×1=2;
設“方程有實根”為事件A,所對應的區域為A={(a,b)|-1≤a≤1,0≤b≤1,b≤a
2},
其面積S
A=
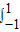
a
2da=

a
3 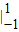
=

,
這是一個幾何概型,所以P(A)=
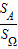
=

.
故選A.
點評:古典概型和幾何概型是我們學習的兩大概型,古典概型要求能夠列舉出所有事件和發生事件的個數,而不能列舉的就是幾何概型,概率的值是通過長度、面積、和體積的比值得到.




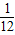
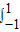 a2da=
a2da= a3
a3 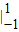 =
= ,
,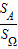 =
= .
.

 互動英語系列答案
互動英語系列答案