
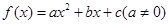 滿足條件:①當(dāng)
滿足條件:①當(dāng)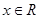 時,
時,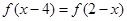 ,且
,且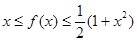 ;②
;② 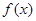 在
在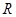 上的最小值為
上的最小值為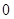 。(1)求
。(1)求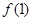 的值及
的值及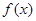 的解析式;(2)若
的解析式;(2)若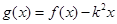 在
在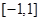 上是單調(diào)函數(shù),求
上是單調(diào)函數(shù),求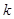 的取值范圍;(3)求最大值
的取值范圍;(3)求最大值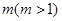 ,使得存在
,使得存在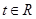 ,只要
,只要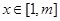 ,就有
,就有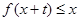 。
。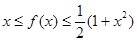 在
在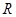 上恒成立,∴
上恒成立,∴
 ……………(1分)
……………(1分)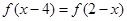 ,∴函數(shù)圖象關(guān)于直線
,∴函數(shù)圖象關(guān)于直線 對稱,
對稱, ……………(2分)
……………(2分) ,∴
,∴
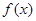 在
在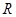 上的最小值為
上的最小值為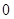 ,∴
,∴ ,即
,即 ,……………(3分)
,……………(3分)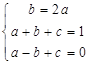 解得
解得 ,∴
,∴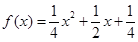 ;……………(4分)
;……………(4分)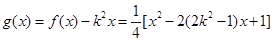 ,
, 對稱軸方程為
對稱軸方程為 ,……………(5分)
,……………(5分) 在
在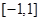 上是單調(diào)函數(shù),∴
上是單調(diào)函數(shù),∴ 或
或 ,……………(7分)
,……………(7分)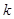 的取值范圍是
的取值范圍是 或
或 或
或 。……………(8分)
。……………(8分)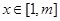 時,
時, 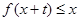 恒成立,∴
恒成立,∴ 且
且 ,
, 得
得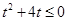 ,解得
,解得 ……………(9分)
……………(9分) 得:
得: ,
, ,……………(10分)
,……………(10分) ,∴
,∴ ,……………(11分)
,……………(11分) 時,對于任意
時,對于任意 ,恒有
,恒有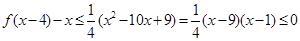 ,
, 的最大值為
的最大值為 .……………(12分)
.……………(12分)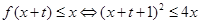 且
且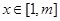

 在
在 上恒成立
上恒成立

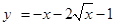 在
在 上遞減,∴
上遞減,∴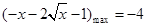 ,
,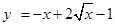 在
在 上遞減,∴
上遞減,∴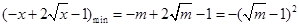
 ,∴
,∴ ,
, ,∵
,∵ ,∴
,∴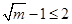 ,
, ,∴
,∴ 的最大值為
的最大值為


 期末好成績系列答案
期末好成績系列答案 99加1領(lǐng)先期末特訓(xùn)卷系列答案
99加1領(lǐng)先期末特訓(xùn)卷系列答案 百強名校期末沖刺100分系列答案
百強名校期末沖刺100分系列答案 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案 金狀元績優(yōu)好卷系列答案
金狀元績優(yōu)好卷系列答案科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
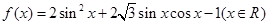 .
.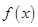 的圖像是由函數(shù)
的圖像是由函數(shù)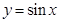 的圖像經(jīng)過怎樣的變換得到的;
的圖像經(jīng)過怎樣的變換得到的;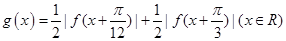 ,試判斷函數(shù)
,試判斷函數(shù)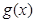 的奇偶性,并用反證法證明函數(shù)
的奇偶性,并用反證法證明函數(shù)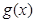 的最小正周期是
的最小正周期是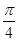 ;
;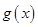 的單調(diào)區(qū)間和值域.
的單調(diào)區(qū)間和值域.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
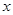 (百萬元)請李子恒老師進(jìn)行創(chuàng)作,經(jīng)調(diào)研知:該唱片的總利潤
(百萬元)請李子恒老師進(jìn)行創(chuàng)作,經(jīng)調(diào)研知:該唱片的總利潤 (百萬元)與
(百萬元)與 成正比的關(guān)系,當(dāng)
成正比的關(guān)系,當(dāng) 時
時 .又有
.又有 ,其中
,其中 是常數(shù),且
是常數(shù),且 .
. ,求其表達(dá)式,定義域(用
,求其表達(dá)式,定義域(用 表示);
表示); 的最大值及相應(yīng)的
的最大值及相應(yīng)的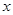 的值.
的值.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
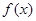 和
和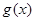 對其定義域上的任意實數(shù)x恒有:
對其定義域上的任意實數(shù)x恒有: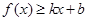 和
和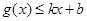 ,則稱直線
,則稱直線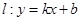 為
為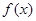 和
和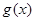 的“隔離直線”。
的“隔離直線”。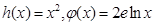 ,則可推知
,則可推知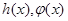 的“隔離直線”方程為 ▲
的“隔離直線”方程為 ▲ 查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com