科目：高中數學 來源： 題型：
設M是由滿足下列兩個條件的函數
構成的集合：
①議程
有實根；②函數的導數
滿足0<<1.
（I）若
，判斷方程的根的個數；
（II）判斷（I）中的函數是否為集合M的元素；
（III）對于M中的任意函數，設x1是方程的實根，求證：對于定義域中任意的x2，x3，當| x2－x1|<1，且| x3－x1|<1時，有
查看答案和解析>>
科目：高中數學 來源：2013屆安徽懷遠縣包集中學高二下學期期中考試理科數學試卷（解析版） 題型：填空題
有下列命題：
①；到兩個定點
距離的和等于定長的點的軌跡是橢圓；
②命題“若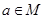
，則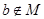
”的逆否命題是：若
；
③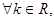
曲線
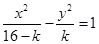表示雙曲線
④設集合M = {x | 0< x ≤3},N = {x | 0< x ≤2},則“a∈M”是“a∈N”的充分而不必要條件則上述命題中真命題為 （填上序號）
查看答案和解析>>
科目：高中數學 來源： 題型：
已知函數f(x)＝lnx＋x2. (1)若函數g(x)＝f(x)－ax在定義域內為增函數，求實數a的取值范圍； (2)在(1)的條件下，若a>1，h(x)＝e3x－3aex，x∈[0，ln2]，求h(x)的極小值； (3)設F(x)＝2f(x)－3x2－kx(k∈R)，若函數F(x)存在兩個零點m，n(0<m<n)，且滿足2x0＝m＋n，問：函數F(x)在(x0，F(x0))處的切線能否平行于x軸？若能，求出該切線方程，若不能，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
已知函數f(x)＝lnx＋x2. (1)若函數g(x)＝f(x)－ax在定義域內為增函數，求實數a的取值范圍； (2)在(1)的條件下，若a>1，h(x)＝e3x－3aex，x∈[0，ln2]，求h(x)的極小值； (3)設F(x)＝2f(x)－3x2－kx(k∈R)，若函數F(x)存在兩個零點m，n(0<m<n)，且滿足2x0＝m＋n，問：函數F(x)在(x0，F(x0))處的切線能否平行于x軸？若能，求出該切線方程，若不能，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
與
垂直，則
的最大值為 .
