
請思考如何利用導數進行求和.
1.Sn=1+2x+3x2+…+nxn-1(x≠0,n∈N*);
2.Sn=![]() +…+n
+…+n![]() (n∈N*).
(n∈N*).
|
導思:1.一般很容易想到通過錯位相減的方法及構造二項式定理的方法來解決,轉換思維角度.由求導公式(xn)=nxn-1可聯想到它們是另外一個和式的導數,因此可轉化求和.利用導數運算,可使問題解法更加簡捷. 2.通過對數列的通項進行聯想,合理運用了逆向思維的方法,從而激發了思維的靈活性,使數列的求和問題得到解決,其關鍵是抓住了數列通項的形式結構,這也有助于培養善于聯想的好習慣. 探究:1.當x=1時,Sn=1+2+3+…+n= (x+x2+x3+…+xn 即Sn=1+2x+3x2+…+nxn-1= 2.(1+x)n=1+ 令x=1,得n·2n-1= 即Sn= |


 智趣寒假作業云南科技出版社系列答案
智趣寒假作業云南科技出版社系列答案科目:高中數學 來源:2013屆遼寧省高二下學期期中考試文科數學試卷(解析版) 題型:解答題
已知函數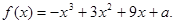
(Ⅰ)求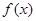 的單調減區間;
的單調減區間;
(Ⅱ)若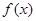 在區間[-2,2].上的最大值為20,求它在該區間上的最小值.
在區間[-2,2].上的最大值為20,求它在該區間上的最小值.
【解析】(1)求導令導數小于零.
(2)利用導數列表求極值,最值即可.
查看答案和解析>>
科目:高中數學 來源:2013屆四川省高二下學期期中考試理科數學試卷(解析版) 題型:解答題
已知函數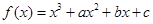 ,曲線
,曲線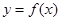 在點
在點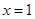 處的切線為
處的切線為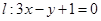 ,若
,若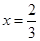 時,
時,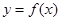 有極值.
有極值.
(1)求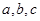 的值;
的值;
(2)求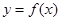 在
在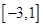 上的最大值和最小值.
上的最大值和最小值.
【解析】(1)根據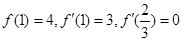 可建立關于a,b,c的三個方程,解方程組即可.
可建立關于a,b,c的三個方程,解方程組即可.
(2)在(1)的基礎上,利用導數列表求極值,最值即可.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com