
【題目】微信紅包是一款可以實現收發紅包、查收記錄和提現的手機應用.某網絡運營商對甲、乙兩個品牌各5種型號的手機在相同環境下,對它們搶到的紅包個數進行統計,得到如表數據:
型號 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ |
甲品牌(個) | 4 | 3 | 8 | 6 | 12 |
乙品牌(個) | 5 | 7 | 9 | 4 | 3 |
(Ⅰ)如果搶到紅包個數超過5個的手機型號為“優”,否則“非優”,請據此判斷是否有85%的把握認為搶到的紅包個數與手機品牌有關?
(Ⅱ)如果不考慮其它因素,要從甲品牌的5種型號中選出3種型號的手機進行大規模宣傳銷售.
①求在型號Ⅰ被選中的條件下,型號Ⅱ也被選中的概率;
②以X表示選中的手機型號中搶到的紅包超過5個的型號種數,求隨機變量X的分布列及數學期望E(X).
下面臨界值表供參考:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
參考公式:K2= ![]() .
.
【答案】解:(Ⅰ)根據題意列出2×2列聯表如下:
紅包個數 手機品牌 | 優 | 非優 | 合計 |
甲品牌(個) | 3 | 2 | 5 |
乙品牌(個) | 2 | 3 | 5 |
合計 | 5 | 5 | 10 |
![]() ,
,
所以沒有85%的理由認為搶到紅包個數與手機品牌有關.
(Ⅱ)①令事件C為“型號 I被選中”;事件D為“型號 II被選中”,
則 ![]() ,
,
所以 ![]() .
.
②隨機變量X的所有可能取值為1,2,3,
![]() ;
;
![]() ;
;
![]() .
.
故X的分布列為:
X | 1 | 2 | 3 |
P | | | |
∴數學期望E(X), ![]() .
.
【解析】(Ⅰ)根據題意列出2×2列聯表,根據2×2列聯表,代入求臨界值的公式,求出觀測值,利用觀測值同臨界值表進行比較,K2=0.4<2.706,可得到沒有足夠的理由認為手機系統與咻得紅包總金額的多少有關;(Ⅱ)由題意求得X的取值1,2,3,運用排列組合的知識,可得各自的概率,求得X的分布列,由期望公式計算即可得到(X).


 作業輔導系列答案
作業輔導系列答案 同步學典一課多練系列答案
同步學典一課多練系列答案 經典密卷系列答案
經典密卷系列答案 金牌課堂練系列答案
金牌課堂練系列答案科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,直線l1的參數方程為 ![]() ,(t為參數),直線l2的參數方程為
,(t為參數),直線l2的參數方程為  ,(m為參數).設l1與l2的交點為P,當k變化時,P的軌跡為曲線C.
,(m為參數).設l1與l2的交點為P,當k變化時,P的軌跡為曲線C.
(1)寫出C的普通方程;
(2)以坐標原點為極點,x軸正半軸為極軸建立極坐標系,設l3:ρ(cosθ+sinθ)﹣ ![]() =0,M為l3與C的交點,求M的極徑.
=0,M為l3與C的交點,求M的極徑.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點M(2,2),N(5,-2),點P在x軸上,分別求滿足下列條件的點P的坐標.
(1)∠MOP=∠OPN(O是坐標原點).
(2)∠MPN是直角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知棱長為1的正方體ABCD-A1B1C1D1中,點E,F,M分別是AB,AD,AA1的中點,又P,Q分別在線段A1B1,A1D1上,且A1P=A1Q=x,0<x<1,設平面MEF∩平面MPQ=l,則下列結論中不成立的是 ( )
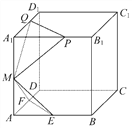
A. l∥平面ABCD
B. l⊥AC
C. 平面MEF與平面MPQ不垂直
D. 當x變化時,l不是定直線
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高校大一新生中的6名同學打算參加學校組織的“演講團”、“吉他協會”等五個社團,若每名同學必須參加且只能參加1個社團且每個社團至多兩人參加,則這6個人中沒有人參加“演講團”的不同參加方法數為( )
A.3600
B.1080
C.1440
D.2520
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某幾何體的俯視圖是如圖所示的矩形,正視圖是一個底邊長為8、高為4的等腰三角形,側視圖是一個底邊長為6、高為4的等腰三角形.

(1)求該幾何體的體積![]() ;
;
(2)求該幾何體的表面積![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,已知正方體ABCD-A1B1C1D1.
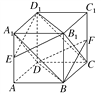
(1)求證:平面A1BD∥平面B1D1C.
(2)若E,F分別是AA1,CC1的中點,求證:平面EB1D1∥平面FBD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xoy中,曲線C1: ![]() (t為參數,t≠0),其中0≤α<π,在以O為極點,x軸正半軸為極軸的極坐標系中,曲線C2:ρ=2sinθ,曲線C3:ρ=2
(t為參數,t≠0),其中0≤α<π,在以O為極點,x軸正半軸為極軸的極坐標系中,曲線C2:ρ=2sinθ,曲線C3:ρ=2 ![]() cosθ. (Ⅰ)求C2與C3交點的直角坐標;
cosθ. (Ⅰ)求C2與C3交點的直角坐標;
(Ⅱ)若C2與C1相交于點A,C3與C1相交于點B,求|AB|的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了研究一種昆蟲的產卵數y和溫度x是否有關,現收集了7組觀測數據列于下表中,并做出了散點圖,發現樣本點并沒有分布在某個帶狀區域內,兩個變量并不呈現線性相關關系,現分別用模型① ![]() 與模型;②
與模型;② ![]() 作為產卵數y和溫度x的回歸方程來建立兩個變量之間的關系.
作為產卵數y和溫度x的回歸方程來建立兩個變量之間的關系.
溫度x/°C | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
產卵數y/個 | 6 | 10 | 21 | 24 | 64 | 113 | 322 |
t=x2 | 400 | 484 | 576 | 676 | 784 | 900 | 1024 |
z=lny | 1.79 | 2.30 | 3.04 | 3.18 | 4.16 | 4.73 | 5.77 |
| | | |
26 | 692 | 80 | 3.57 |
| | | |
1157.54 | 0.43 | 0.32 | 0.00012 |
其中 ![]() ,
, ![]() ,zi=lnyi ,
,zi=lnyi , ![]() ,
,
附:對于一組數據(μ1 , ν1),(μ2 , ν2),(μn , νn),其回歸直線v=βμ+α的斜率和截距的最小二乘估計分別為:  ,
, ![]()
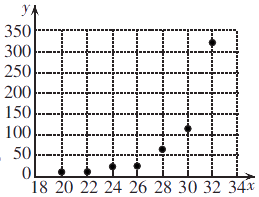
(1)根據表中數據,分別建立兩個模型下y關于x的回歸方程;并在兩個模型下分別估計溫度為30°C時的產卵數.(C1 , C2 , C3 , C4與估計值均精確到小數點后兩位)(參考數據:e4.65≈104.58,e4.85≈127.74,e5.05≈156.02)
(2)若模型①、②的相關指數計算分別為 ![]() .,請根據相關指數判斷哪個模型的擬合效果更好.
.,請根據相關指數判斷哪個模型的擬合效果更好.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com