
當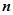 為正整數時,定義函數
為正整數時,定義函數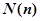 表示
表示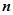 的最大奇因數.如
的最大奇因數.如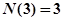 ,
,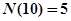 ,….記
,….記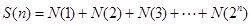 .則
.則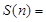 .(用
.(用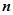 來表示)
來表示)
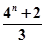
【解析】
試題分析:由N(x)的性質可得知,當x是奇數時,x的最大奇數因子明顯是它本身.因此N(x)=x,因此,我們就可將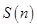 進行分解,分別算出奇數項的和與偶數項的和進而相加,即
進行分解,分別算出奇數項的和與偶數項的和進而相加,即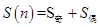 ,
,
所以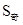 =N(1)+N(3)+…+N(
=N(1)+N(3)+…+N(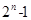 )=1+3+…+
)=1+3+…+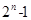 =
= 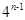 。
。
當x是偶數時,且x∈[ )
)
①當k=1時,x∈[2,4)該區間包含的偶數只有2,而N(2)=1所以該區間所有的偶數的最大奇因數之和為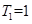 ;
;
②當k=2時,x∈[4,8),該區間包含的偶數為4,6,所以該區間所有的最大奇因數偶數之和為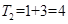
③當k=3時,x∈[8,16),該區間包含的偶數為8,10.,12,14,則該區間所有偶數的最大奇因數之和為 ,因此我們可以用數學歸納法得出當x∈[
,因此我們可以用數學歸納法得出當x∈[ )該區間所有偶數的最大奇因數和
)該區間所有偶數的最大奇因數和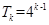
∴對k從1到n-1求和得
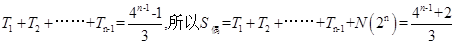 ,
,
綜上知: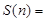
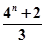 。
。
考點:數列的綜合應用。
點評:本題主要考查了數列的求和問題.考查了學生通過已知條件分析問題和解決問題的能力.


科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com