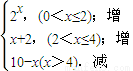Question

用min{a，b，c}表示a，b，c三個數中的最小值，設f（x）=min{2^x，x+2，10-x}（x≥0），則f（x）的最大值為（ ）
A．7
B．6
C．5
D．4

Answer 1

【答案】分析：畫出函數圖象，觀察最大值的位置，通過求函數值，解出最大值．
解答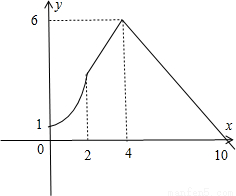：解：畫出y=2^x，y=x+2，y=10-x的圖象，
觀察圖象可知，當0≤x≤2時，f（x）=2^x，
當2≤x≤4時，f（x）=x+2，
當x＞4時，f（x）=10-x，
f（x）的最大值在x=4時取得為6，
故選B．
點評：本題考查了函數最值問題，利用數形結合可以很容易的得到最大值．
也可以利用函數單調性，解法如下：
由x+2-（10-x）=2x-8≥0，得x≥4．
0＜x≤2時2^x-（x+2）≤0，2^x≤2+x＜10-x，f（x）=2^x；
2＜x≤4時，x+2＜2^x，x+2≤10-x，f（x）=x+2；
由2^x+x-10=0得x₁≈2.84
x＞x₁時2^x＞10-x，x＞4時x+2＞10-x，f（x）=10-x．
綜上，f（x）=
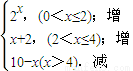
∴f（x）max=f（4）=6．選B．