設函數f(x)=x3+bx2+cx+5,且曲線y=f(x)在點(0,f(0))處的切線與x軸平行.
(Ⅰ)求實數c的值;
(Ⅱ)判斷是否存在實數b,使得方程f(x)-b2x=0恰有一個實數根.若存在,求b的取值范圍;若不存在,請說明理由.
解:(I)∵曲線y=f(x)在點(0,f(0))處的切線與x軸平行,∴f'(0)=0.
又f'(x)=3x
2+2bx+c,則f'(0)=c=0.
(II)由c=0,方程f(x)-b
2x=0可化為x
3+bx
2-b
2x+5=0,假設存在實數b使得此方程恰有一個實數根,則令g(x)=x
3+bx
2-b
2x+5,只需g(x)
極大值<0或g(x)
極小值>0
∴g'(x)=3x
2+2bx-b
2=(3x-b)(x+b)令g'(x)=0,得
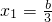
,x
2=-b
①若b=0,則方程f(x)-b
2x=0可化為x
3+5=0,此方程恰有一個實根

②若b>0,則
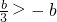
,列表:
| x | (-∞,-b) | -b | 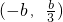 |  | 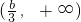 |
| g'(x) | + | 0 | - | 0 | + |
| g(x) | ↗ | 極大值 | ↘ | 極小值 | ↗ |
∴g(x)
極大值=g(-b)=b
3+5>0,
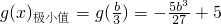
∴
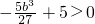
,解之得0<b<3
③若b<0,則
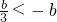
,列表:
| x |  |  |  | -b | (-b,+∞) |
| g'(x) | + | 0 | - | 0 | + |
| g(x) | ↗ | 極大值 | ↘ | 極小值 | ↗ |
∴
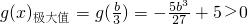
,g(x)
極小值=g(-b)=b
3+5
∴b
3+5>0,解之得
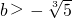
∴
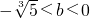
綜合①②③可得,實數b的取值范圍是
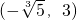
.
分析:(I)曲線y=f(x)在點(0,f(0))處的切線與x軸平行,可得f'(0)=0.從而可求
(II)若使方程f(x)-b
2x=x
3+bx
2-b
2x+5=0恰有一個實數根.構造函數g(x)=x
3+bx
2-b
2x+5,只需g(x)
極大值<0或g(x)
極小值>0,利用導數可求
點評:本題主要考查了利用函數的導數求解曲線的在某點處的切線的斜率,函數的極大(小)值的求解,還要注意方程與函數的相互轉化的思想在解題中的應用.

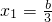 ,x2=-b
,x2=-b
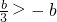 ,列表:
,列表: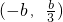

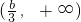
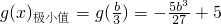
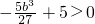 ,解之得0<b<3
,解之得0<b<3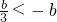 ,列表:
,列表:


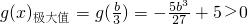 ,g(x)極小值=g(-b)=b3+5
,g(x)極小值=g(-b)=b3+5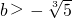
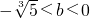
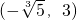 .
.
