【題目】已知直線l：mx﹣y=1，若直線l與直線x﹣（m﹣1）y=2垂直，則m的值為 ， 動直線l：mx﹣y=1被圓C：x2﹣2x+y2﹣8=0截得的最短弦長為 ．
【答案】
；2 
【解析】解：∵直線l：mx﹣y=1，直線l與直線x﹣（m﹣1）y=2垂直，
∴m×1+（﹣1）×[﹣（m﹣1）]=0，
解得m= 
．
∵圓C：x2﹣2x+y2﹣8=0的圓心C（1，0），半徑r= 
=3，
圓心C（1，0）到直線l：mx﹣y=1的距離d= 
，
∴弦長為：2 
=2 
=2 
，
∴當且僅當m=﹣1時，動直線l：mx﹣y=1被圓C：x2﹣2x+y2﹣8=0截得的最短弦長為2 
．
所以答案是： 
．
【考點精析】利用直線與圓的三種位置關系對題目進行判斷即可得到答案，需要熟知直線與圓有三種位置關系：無公共點為相離；有兩個公共點為相交,這條直線叫做圓的割線；圓與直線有唯一公共點為相切，這條直線叫做圓的切線，這個唯一的公共點叫做切點．
智趣暑假溫故知新系列答案科目：高中數學 來源： 題型：
【題目】已知直線l的參數方程為 
（t為參數），曲線C的參數方程為 
（θ為參數），以坐標原點為極點，x軸的正半軸為極軸建立極坐標系，點P的極坐標為（2 
， 
）．
（Ⅰ）求直線l以及曲線C的極坐標方程；
（Ⅱ）設直線l與曲線C交于A，B兩點，求△PAB的面積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=sinx，x∈（0，2π），點P（x，y）是函數f（x）圖象上任一點，其中0（0，0），A（2π，0），記△OAP的面積為g（x），則g′（x）的圖象可能是（ ）
A.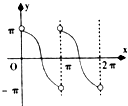
B.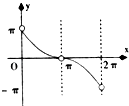
C.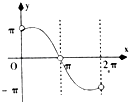
D.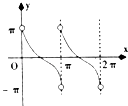
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=m﹣|x﹣2|，m∈R，且f（x+2）≥0的解集為[﹣1，﹣1]．
（1）求m的值；
（2）若a，b，c∈R，且 
+ 
+ 
=m，求證：a2+b2+c2≥36．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線l：x＋2y－2＝0，試求：
（1）點P(－2，－1)關于直線l的對稱點坐標；
（2）直線 
關于直線l對稱的直線l2的方程；
（3）直線l關于點(1，1)對稱的直線方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】直線l1 ， l2分別是函數f（x）=sinx，x∈[0，π]圖象上點P1 ， P2處的切線，l1 ， l2垂直相交于點P，且l1 ， l2分別與y軸相交于點A，B，則△PAB的面積為
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
