
【題目】函數y=f(x)是定義在a,b上的增函數,其中a,b∈R且0<b<﹣a,已知y=f(x)無零點,設函數F(x)=f2(x)+f2(﹣x),則對于F(x)有以下四個說法:
①定義域是[﹣b,b];②是偶函數;③最小值是0;④在定義域內單調遞增.
其中正確的有(填入你認為正確的所有序號)
【答案】①②
【解析】解:根據題意,依次分析4個命題:
對于①,對于F(x)=f2(x)+f2(﹣x),有a≤x≤b,a≤﹣x≤b,
而又由0<b<﹣a,則F(x)=f2(x)+f2(﹣x)中,x的取值范圍是﹣b≤x≤b,即其定義域是[﹣b,b],則①正確;
對于②,F(﹣x)=f2(﹣x)+f2(x)=F(x),且其定義域為[﹣b,b],關于原點對稱,
則F(x)為偶函數,②正確;
對于③,由y=f(x)無零點,假設f(x)=2x , F(x)=22x+2﹣2x=22x+ ![]() ≥2,其最小值為2,故③錯誤;
≥2,其最小值為2,故③錯誤;
對于④,由于F(x)是偶函數,則F(x)在[﹣b,0]上與[0,b]上的單調性相反,故F(x)在其定義域內不會單調遞增,④錯誤;
所以答案是①②.
【考點精析】根據題目的已知條件,利用函數的定義域及其求法和函數的值域的相關知識可以得到問題的答案,需要掌握求函數的定義域時,一般遵循以下原則:①![]() 是整式時,定義域是全體實數;②
是整式時,定義域是全體實數;②![]() 是分式函數時,定義域是使分母不為零的一切實數;③
是分式函數時,定義域是使分母不為零的一切實數;③![]() 是偶次根式時,定義域是使被開方式為非負值時的實數的集合;④對數函數的真數大于零,當對數或指數函數的底數中含變量時,底數須大于零且不等于1,零(負)指數冪的底數不能為零;求函數值域的方法和求函數最值的常用方法基本上是相同的.事實上,如果在函數的值域中存在一個最小(大)數,這個數就是函數的最小(大)值.因此求函數的最值與值域,其實質是相同的.
是偶次根式時,定義域是使被開方式為非負值時的實數的集合;④對數函數的真數大于零,當對數或指數函數的底數中含變量時,底數須大于零且不等于1,零(負)指數冪的底數不能為零;求函數值域的方法和求函數最值的常用方法基本上是相同的.事實上,如果在函數的值域中存在一個最小(大)數,這個數就是函數的最小(大)值.因此求函數的最值與值域,其實質是相同的.


科目:高中數學 來源: 題型:
【題目】首項為正數的數列{an}滿足an+1=(a+3),n∈N*.
(1)證明:若a1為奇數,則對一切n≥2,an都是奇數;
(2)若對一切n∈N*都有an+1>an , 求a1的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來城市“共享單車”的投放在我國各地迅猛發展,“共享單車”為人們出行提供了很大的便利,但也給城市的管理帶來了一些困難,現某城市為了解人們對“共享單車”投放的認可度,對![]() 年齡段的人群隨機抽取
年齡段的人群隨機抽取![]() 人進行了一次“你是否贊成投放共享單車”的問卷調查,根據調查結果得到如下統計表和各年齡段人數頻率分布直方圖:
人進行了一次“你是否贊成投放共享單車”的問卷調查,根據調查結果得到如下統計表和各年齡段人數頻率分布直方圖:
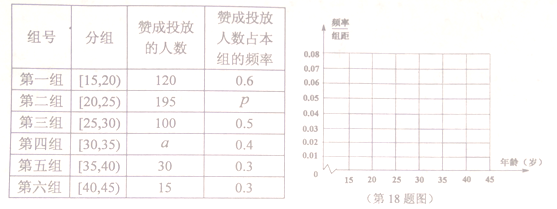
(1)補全頻率分布直方圖,并求![]() 的值;
的值;
(2)在第四、五、六組“贊成投放共享單車”的人中,用分層抽樣的方法抽取7人參加“共享單車”騎車體驗活動,求第四、五、六組應分別抽取的人數;
(3)在(2)中抽取的7人中隨機選派2人作為正副隊長,求所選派的2人沒有第四組人的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設集合S={A0 , A1 , A2 , A3},在S上定義運算⊕:Ai⊕Aj=Ak , 其中k為i+j被4除的余數,i,j=0,1,2,3,則使關系式(Ai⊕Ai)⊕Aj=A0成立的有序數對(i,j)的組數為( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,兩個橢圓![]() ,
, ![]() 內部重疊區域的邊界記為曲線C,P是曲線C上的任意一點,給出下列四個判斷:
內部重疊區域的邊界記為曲線C,P是曲線C上的任意一點,給出下列四個判斷:
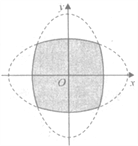
①P到F1(-4,0)、F2(4,0)、E1(0,-4)、E2(0,4)四點的距離之和為定值;
②曲線C關于直線y=x、y=-x均對稱;③曲線C所圍區域面積必小于36.
④曲線C總長度不大于6π.上述判斷中正確命題的序號為________________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com