
【題目】教材上一例問題如下:
一只紅鈴蟲的產卵數y和溫度x有關,現收集了7組觀測數據如下表,試建立y與x之間的回歸方程.
溫度 x/℃ | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
產卵數y/個 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
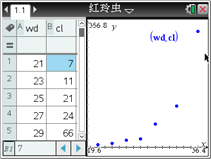
某同學利用圖形計算器研究它時,先作出散點圖(如圖所示),發現兩個變量不呈線性相關關系. 根據已有的函數知識,發現樣本點分布在某一條指數型曲線![]() 的附近(
的附近(![]() 和
和![]() 是待定的參數),于是進行了如下的計算:
是待定的參數),于是進行了如下的計算:
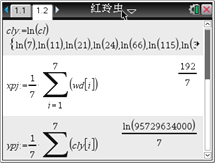
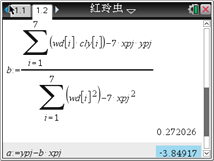
根據以上計算結果,可以得到紅鈴蟲的產卵數y對溫度x的回歸方程為__________.(精確到0.0001) (提示:![]() 利用代換可轉化為線性關系)
利用代換可轉化為線性關系)
 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:高中數學 來源: 題型:
【題目】為了研究某藥品的療效,選取若干名志愿者進行臨床試驗.所有志愿者的舒張壓數據(單位:kPa)的分組區間為[12,13),[13,14),[14,15),[15,16),[16,17],將其按從左到右的順序分別編號為第一組,第二組,…,第五組.如圖是根據試驗數據制成的頻率分布直方圖.已知第一組與第二組共有20人,第三組中沒有療效的有6人,則第三組中有療效的人數為( ) 
A.6
B.8
C.12
D.18
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙三名大學生參加學校組織的“國學達人”挑戰賽, 每人均有兩輪答題機會,當且僅當第一輪不過關時進行第二輪答題.根據平時經驗,甲、乙、丙三名大學生每輪過關的概率分別為![]() ,且三名大學生每輪過關與否互不影響.
,且三名大學生每輪過關與否互不影響.
(1)求甲、乙、丙三名大學生都不過關的概率;
(2)記![]() 為甲、乙、丙三名大學生中過關的人數,求隨機變量
為甲、乙、丙三名大學生中過關的人數,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某網站從春節期間參與收發網絡紅包的手機用戶中隨機抽取![]() 名進行調查,將受訪用戶按年齡分成
名進行調查,將受訪用戶按年齡分成![]() 組:
組: ![]() ,
, ![]() ,…,
,…, ![]() ,并整理得到如下頻率分布直方圖:
,并整理得到如下頻率分布直方圖:

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)從春節期間參與收發網絡紅包的手機用戶中隨機抽取一人,估計其年齡低于![]() 歲的概率;
歲的概率;
(Ⅲ)估計春節期間參與收發網絡紅包的手機用戶的平均年齡.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某人研究中學生的性別與成績、視力、智商、閱讀量這4個變量的關系,隨機抽查了52名中學生,得到統計數據如表1至表4,則與性別有關聯的可能性最大的變量是( )
表1
成績 | 不及格 | 及格 | 總計 |
男 | 6 | 14 | 20 |
女 | 10 | 22 | 32 |
總計 | 16 | 36 | 52 |
表2
視力 | 好 | 差 | 總計 |
男 | 4 | 16 | 20 |
女 | 12 | 20 | 32 |
總計 | 16 | 36 | 52 |
表3
智商 | 偏高 | 正常 | 總計 |
男 | 8 | 12 | 20 |
女 | 8 | 24 | 32 |
總計 | 16 | 36 | 52 |
表4
閱讀量 | 豐富 | 不豐富 | 總計 |
男 | 14 | 6 | 20 |
女 | 2 | 30 | 32 |
總計 | 16 | 36 | 52 |
A.成績
B.視力
C.智商
D.閱讀量
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD中,ABCD為矩形,平面PAD⊥平面ABCD. 
(1)求證:AB⊥PD;
(2)若∠BPC=90°,PB= ![]() ,PC=2,問AB為何值時,四棱錐P﹣ABCD的體積最大?并求此時平面BPC與平面DPC夾角的余弦值.
,PC=2,問AB為何值時,四棱錐P﹣ABCD的體積最大?并求此時平面BPC與平面DPC夾角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f0(x)= ![]() (x>0),設fn(x)為fn﹣1(x)的導數,n∈N* .
(x>0),設fn(x)為fn﹣1(x)的導數,n∈N* .
(1)求2f1( ![]() )+
)+ ![]() f2(
f2( ![]() )的值;
)的值;
(2)證明:對任意n∈N* , 等式|nfn﹣1( ![]() )+
)+ ![]() fn(
fn( ![]() )|=
)|= ![]() 都成立.
都成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某實驗室一天的溫度(單位:℃)隨時間t(單位:h)的變化近似滿足函數關系:
f(t)=10﹣ ![]() ,t∈[0,24)
,t∈[0,24)
(1)求實驗室這一天的最大溫差;
(2)若要求實驗室溫度不高于11℃,則在哪段時間實驗室需要降溫?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com