
解法一:設銷售價定為每件x元(50<x≤80).
每天獲得利潤y元,則y=(x-50)·P=![]() .
.
設x-50=t,則0<t≤30,
∴y=![]() =
=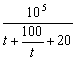 ≤
≤![]() =2500.
=2500.
當且僅當t=10,即x=60時,ymax=2500.
答:每件60元時,每天獲利最多,最多是2500元.
解法二:求y=![]() 的最大值,還可轉化為二次函數的最大值問題解之.
的最大值,還可轉化為二次函數的最大值問題解之.
令![]() =t,∵10<x-40≤40,∴
=t,∵10<x-40≤40,∴![]() ≤t<
≤t<![]() .
.
y=![]() =105·t2(
=105·t2(![]() -10)=105(-10t2+t).
-10)=105(-10t2+t).
當t=![]() ,即x=60時,ymax=2500.
,即x=60時,ymax=2500.
求y的最大值,還可以用二次函數的判別式方法解.
令x-40=t,則10<t≤40,y=![]() ,
,
即yt2-105t+106=0. ①
Δ=1010-4·106·y≥0.
解之y≤2500,即ymax=2500.
檢驗:當y=2500時,方程①2500t2-105t+106=0,即t2-40t+400=0.
解之t=20∈(10,40].
這時x=60.
點評:(1)設變量時,把最值變量定為函數,建立函數關系式.(2)構造相應的數學模型求最值.法一:令x-50=t,使分子最簡,同除以分子后,很容易用均值不等式求分母的最值.法二:令![]() =t,使二次函數式最簡,易于求二次函數y的最值.法三:令x-40=t,應用二次方程判別式求最值.但應注意檢驗.
=t,使二次函數式最簡,易于求二次函數y的最值.法三:令x-40=t,應用二次方程判別式求最值.但應注意檢驗.


科目:高中數學 來源: 題型:044
某商品進貨價每件
50元,據市場調查,當銷售價格(每件x元)在50≤x≤80時,每天售出的件數為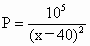 ,若想每天獲得的利潤最多,銷售價格每件應定為多少元?
,若想每天獲得的利潤最多,銷售價格每件應定為多少元?
查看答案和解析>>
科目:高中數學 來源:數學教研室 題型:044
某商品進貨價每件50元,據市場調查,當銷售價格(每件x元)在50≤x≤80時,每天售出的件數為 ,若想每天獲得的利潤最多,銷售價格每件應定為多少元?
,若想每天獲得的利潤最多,銷售價格每件應定為多少元?
查看答案和解析>>
科目:高中數學 來源:2011-2012學年黑龍江省高三上學期期中考試理科數學 題型:解答題
(本小題滿分12分)
某商品進貨價每件50元,據市場調查,當銷售價格(每件x元)為50<x≤80時,每
天售出的件數為 ,若要使每天獲得的利潤最多,銷售價格每件應定為多少元?
,若要使每天獲得的利潤最多,銷售價格每件應定為多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com