
設f(x)是定義在[-1,1]上的偶函數,g(x)與f(x)的圖象關于直線x-1=0對稱.且當x∈[2,3]時,g(x)=2a·(x-2)-4(x-2)3(a為實數)
(1)求函數f(x)的表達式;
(2)在a∈(2,6]或(6,+∞)的情況下,分別討論函數f(x)最大值,并指出a為何值時,f(x)的圖像的最高點恰好落在直線y=12上.
|
(1) (1)當 當
所以, (2)不妨在區間
如果 令f(1)=2a-4=12可解得:a=8 如果 由于x1<x2,要使上式成立,只需: f(x)在區間 所以,f(x)在區間[-1,1]上的最大值為 令 綜上可知:當 并且,當a=8時,函數f(x)的圖像的最高點恰好落在直線y=12上. |
|
(1)注意到g(x)是定義在區間[2,3]上的函數,因此,根據對稱性,我們只能求出f(x)在區間[-1,0]上的解析式,f(x)在區間[0,1]上的解析式,則可以根據函數的奇偶性去求. (2)因為f(x)為偶函數,所以,f(x)(-1≤x≤1)的最大值,必等于f(x)在區間[0,1]上的最大值.故只需考慮0≤x≤1的情形,此時,f(x)=-4x3+2ax.對于這個三次函數,要求其最大值,比較容易想到的方法是:考慮其單調性. |


 教學練新同步練習系列答案
教學練新同步練習系列答案 課前課后同步練習系列答案
課前課后同步練習系列答案 課堂小作業系列答案
課堂小作業系列答案 黃岡小狀元口算速算練習冊系列答案
黃岡小狀元口算速算練習冊系列答案科目:高中數學 來源: 題型:
①y=3-f(x) ②y=1+![]() ③y=[f(x)]2 ④y=1-
③y=[f(x)]2 ④y=1-![]()
A.1 B
查看答案和解析>>
科目:高中數學 來源: 題型:
(1)當x∈(1,3]時,f(x)的表達式;
(2)f(-3)及f(3.5)的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
A.a<-1或a>![]() B.-l<a<
B.-l<a<![]()
C.a<![]() D.a<
D.a<![]() 且a≠-1
且a≠-1
查看答案和解析>>
科目:高中數學 來源:2011-2012學年大綱版高三上學期單元測試(6)數學試卷 題型:解答題
設f(x)是定義在[-1,1]上的奇函數,且對任意的實數a,b∈[-1,1],當a+b
≠0時,都有 >0.
>0.
(1)若a>b,試比較f(a)與f(b)的大小;
(2)解不等式f(x- )<f(x-
)<f(x- );
);
(3)如果g(x)=f(x-c)和h(x)=f(x-c2)這兩個函數的定義域的交集是空集,求c的取值范圍.
查看答案和解析>>
科目:高中數學 來源:江蘇省2010年高考預測試題數學 題型:解答題
設f(x)是定義在[0,1]上的函數,若存在x*∈(0,1),使得f(x)在[0,x*]上單調遞增,在[x*,1]上單調遞減,則稱f(x)為[0,1]上的單峰函數,x*為峰點,包含峰點的區間為含峰區間.對任意的[0,1]上的單峰函數f(x),下面研究縮短其含峰區間長度的方法.
(I)證明:對任意的 ∈(O,1),
∈(O,1), ,若f(
,若f( )≥f(
)≥f(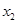 ),則(0,
),則(0,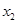 )為含峰區間:若f(
)為含峰區間:若f( )
) f(
f(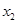 ),則
),則 為含峰區間:
為含峰區間:
(II)對給定的r(0<r<0.5),證明:存在 ∈(0,1),滿足
∈(0,1),滿足 ,使得由(I)所確定的含峰區間的長度不大于0.5+r:
,使得由(I)所確定的含峰區間的長度不大于0.5+r:
(III)選取 ∈(O,1),,由(I)可確定含峰區間為
∈(O,1),,由(I)可確定含峰區間為 或
或 ,在所得的含峰區間內選取
,在所得的含峰區間內選取 ,由
,由 與
與 或
或 與
與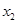 類似地可確定一個新的含峰區間,在第一次確定的含峰區間為(0,
類似地可確定一個新的含峰區間,在第一次確定的含峰區間為(0,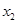 )的情況下,試確定的值
)的情況下,試確定的值 ,滿足兩兩之差的絕對值不小于0.02,且使得新的含峰區間的長度縮短到0. 34(區間長度等于區間的右端點與左端點之差)
,滿足兩兩之差的絕對值不小于0.02,且使得新的含峰區間的長度縮短到0. 34(區間長度等于區間的右端點與左端點之差)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com