解:設圓的方程為:(x-a)
2+(y-b)
2=r
2∵直線2x+y=0平分圓,
則:圓心在直線2x+y=0上,則2a+b=0?b=-2a(2分)
又直線x-y+1=0與圓相交所得的弦長為

,
由圓的幾何性質可得:圓心到該直線的距離為

(2分)
即:
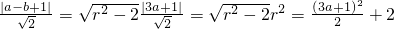
(2分)
∴該圓的方程為
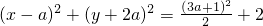
,
把A的坐標(2,3)代入圓的方程得:a
2+10a+21=0,
解得:a=-3或a=-7,
∴圓的方程為:(x+3)
2+(y-6)
2=34或(x+7)
2+(y-14)
2=202.
分析:由圓心為(a,b),半徑為r,設出圓的標準方程,由直線2x+y=0平分圓C得到圓心C在直線上,把圓心的坐標代入已知直線方程用a表示出b,然后根據圓C與直線x-y+1=0相交的弦長,根據垂徑定理及勾股定理,由圓的半徑r及弦長的一半表示出圓心到直線x-y+1=0的距離,利用點到直線的距離公式,表示出圓心到直線x-y+1=0的距離,兩者相等,用a表示出r,將表示出的b和半徑r代入圓的方程消去b和r,再把A的坐標代入圓的方程,即可求出a的值,從而確定出圓的方程.
點評:此題考查了直線與圓相交的性質,垂徑定理、勾股定理及圓的對稱性,點到直線的距離公式,要求學生綜合圓的幾何性質來解決問題,解答此類題常常利用待定系數法來求出圓的標準方程,同時在解答時注意消去參數b和r.

 ,求圓C的方程.
,求圓C的方程. ,
, (2分)
(2分)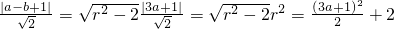 (2分)
(2分)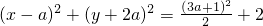 ,
,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案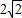 ,求圓C的方程.
,求圓C的方程.