
設函數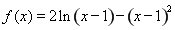 .
.
(1)求函數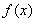 的單調遞增區間;
的單調遞增區間;
(2)若關于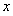 的方程
的方程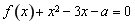 在區間
在區間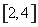 內恰有兩個相異的實根,求實數
內恰有兩個相異的實根,求實數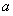 的取值范圍.
的取值范圍.
(1)函數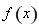 的單調遞增區間為
的單調遞增區間為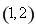 ;(2)
;(2)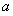 的取值范圍是
的取值范圍是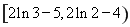 .
.
【解析】
試題分析:(1)確定出函數的定義域是解決本題的關鍵,利用導數作為工具,求出該函數的單調遞增區間即為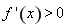 的
的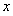 的取值區間;(2)方法一:利用函數思想進行方程根的判定問題是解決本題的關鍵.構造函數,研究構造函數的性質尤其是單調性,列出該方程有兩個相異的實根的不等式組,求出實數
的取值區間;(2)方法一:利用函數思想進行方程根的判定問題是解決本題的關鍵.構造函數,研究構造函數的性質尤其是單調性,列出該方程有兩個相異的實根的不等式組,求出實數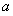 的取值范圍.方法二:先分離變量再構造函數,利用函數的導數為工具研究構造函數的單調性,根據題意列出關于實數
的取值范圍.方法二:先分離變量再構造函數,利用函數的導數為工具研究構造函數的單調性,根據題意列出關于實數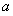 的不等式組進行求解.本題將方程的根的問題轉化為函數的圖象交點問題,是解決問題的關鍵.
的不等式組進行求解.本題將方程的根的問題轉化為函數的圖象交點問題,是解決問題的關鍵.
試題解析:(1)函數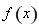 的定義域為
的定義域為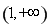 , 1分
, 1分
∵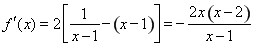 , 2分
, 2分
∵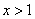 ,則使
,則使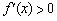 的
的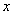 的取值范圍為
的取值范圍為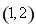 ,
,
故函數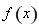 的單調遞增區間為
的單調遞增區間為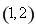 . 4分
. 4分
(2)方法1:∵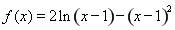 ,
,
∴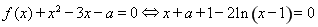 . 6分
. 6分
令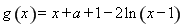 ,
,
∵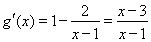 ,且
,且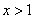 ,
,
由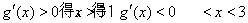 .
.
∴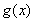 在區間
在區間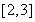 內單調遞減,在區間
內單調遞減,在區間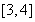 內單調遞增, 9分
內單調遞增, 9分
故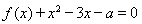 在區間
在區間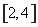 內恰有兩個相異實根
內恰有兩個相異實根 12分
12分
即 解得:
解得: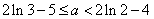 .
.
綜上所述,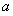 的取值范圍是
的取值范圍是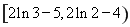 . 14分
. 14分
方法2:∵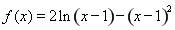 ,
,
∴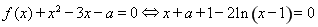 . 6分
. 6分
即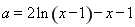 ,
,
令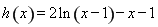 ,
,
∵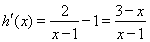 ,且
,且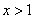 ,
,
由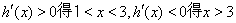 .
.
∴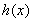 在區間
在區間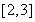 內單調遞增,在區間
內單調遞增,在區間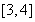 內單調遞減. 9分
內單調遞減. 9分
∵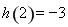 ,
,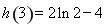 ,
,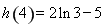 ,
,
又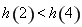 ,
,
故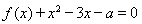 在區間
在區間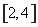 內恰有兩個相異實根
內恰有兩個相異實根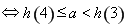 . 12分
. 12分
即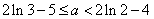 .
.
綜上所述,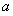 的取值范圍是
的取值范圍是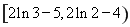 . 14分
. 14分
考點:函數與方程的綜合運用;利用導數研究函數的單調性.


 金鑰匙試卷系列答案
金鑰匙試卷系列答案科目:高中數學 來源:2013-2014學年高中數學人教A版選修4-1知能達標2-4練習卷(解析版) 題型:選擇題
如圖所示,經過⊙O上的點A的切線和弦BC的延長線相交于點P,若∠CAP=40°,∠ACP=100°,則∠BAC所對的弧的度數為
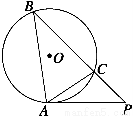
A.40° B.100° C.120° D.30°
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高中數學人教A版選修4-1知能達標1-4練習卷(解析版) 題型:選擇題
在△ABC中,∠BAC=90°,AD是BC邊上的高,則相似三角形共有
A.0對 B.1對 C.2對 D.3對
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高中數學人教A版選修4-1知能達標1-2練習卷(解析版) 題型:填空題
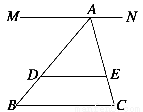
如圖所示,在△ABC中,MN∥DE∥BC,若AE∶EC=7∶3,則DB∶AB的值為________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高中數學人教A版選修4-1知能達標1-1練習卷(解析版) 題型:填空題
已知梯形的中位線長10 cm,一條對角線將中位線分成的兩部分之差是3 cm,則該梯形中的較大的底是________ cm.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年陜西西安第一中學高三第二學期第二次模擬考試理科數學試卷(解析版) 題型:解答題
設函數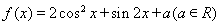 .
.
(1)求函數 的最小正周期和單調遞增區間;
的最小正周期和單調遞增區間;
(2)當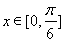 時,
時, 的最大值為2,求
的最大值為2,求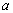 的值,并求出
的值,并求出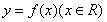 的對稱軸方程.
的對稱軸方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com