
【題目】已知向量 ![]() ,
, ![]() ,且
,且 ![]() ,f(x)=
,f(x)= ![]()
![]() ﹣2λ|
﹣2λ| ![]() |(λ為常數), 求:
|(λ為常數), 求:
(1)![]()
![]() 及|
及| ![]() |;
|;
(2)若f(x)的最小值是 ![]() ,求實數λ的值.
,求實數λ的值.
【答案】
(1)解: ![]() ,
, ![]() ,
,
∵ ![]() ,
,
∴cosx≥0,
∴ ![]()
(2)解:f(x)=cos2x﹣4λcosx=2(cosx﹣λ)2﹣1﹣2λ2,
∵ ![]() ,
,
∴0≤cosx≤1,
①當λ<0時,當且僅當cosx=0時,f(x)取得最小值﹣1,這與已知矛盾;
②當0≤λ≤1,當且僅當cosx=λ時,f(x)取得最小值﹣1﹣2λ2,
由已知得 ![]() ,解得
,解得 ![]() ;
;
③當λ>1時,當且僅當cosx=1時,f(x)取得最小值1﹣4λ,
由已知得 ![]() ,解得
,解得 ![]() ,這與λ>1相矛盾、
,這與λ>1相矛盾、
綜上所述, ![]() 為所求
為所求
【解析】(1)根據所給的向量的坐標,寫出兩個向量的數量積,寫出數量積的表示式,利用三角函數變換,把數量積整理成最簡形式,再求兩個向量和的模長,根據角的范圍,寫出兩個向量的模長.(2)根據第一問做出的結果,寫出函數的表達式,式子中帶有字母系數λ,把式子整理成關于cosx的二次函數形式,結合λ的取值范圍,寫出函數式的最小值,是它的最小值等于已知量,得到λ的值,把不合題意的舍去.


科目:高中數學 來源: 題型:
【題目】已知點A(﹣ ![]() ,0),B(
,0),B( ![]() ,0),P是平面內的一個動點,直線PA與PB交于點P,且它們的斜率之積是﹣
,0),P是平面內的一個動點,直線PA與PB交于點P,且它們的斜率之積是﹣ ![]() .
.
(1)求動點P的軌跡C的方程;
(2)設直線l:y=kx+1與曲線C交于M、N兩點,當線段MN的中點在直線x+2y=0上時,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C的圓心在坐標原點,且與直線l1:x﹣y﹣2 ![]() =0相切 (Ⅰ)求直線l2:4x﹣3y+5=0被圓C所截得的弦AB的長.
=0相切 (Ⅰ)求直線l2:4x﹣3y+5=0被圓C所截得的弦AB的長.
(Ⅱ)過點G(1,3)作兩條與圓C相切的直線,切點分別為M,N,求直線MN的方程
(Ⅲ) 若與直線l1垂直的直線l與圓C交于不同的兩點P,Q,若∠POQ為鈍角,求直線l縱截距的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),|
=(cosβ,sinβ),| ![]() ﹣
﹣ ![]() |=
|= ![]() .
.
(1)求cos(α﹣β)的值;
(2)若0<α< ![]() ,﹣
,﹣ ![]() <β<0,且sinβ=﹣
<β<0,且sinβ=﹣ ![]() ,求sinα的值.
,求sinα的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】渝州集團對所有員工進行了職業技能測試從甲、乙兩部門中各任選10名員工的測試成績(單位:分)數據的莖葉圖如圖所示.
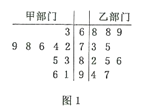
(1)若公司決定測試成績高于85分的員工獲得“職業技能好能手”稱號,求從這20名員工中任選三人,其中恰有兩人獲得“職業技能好能手”的概率;
(2)公司結合這次測試成績對員工的績效獎金進行調整(績效獎金方案如下表),若以甲部門這10人的樣本數據來估計該部門總體數據,且以頻率估計概率,從甲部門所有員工中任選3名員工,記績效獎金不小于![]() 的人數為
的人數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法:
①若f(x)=ax2+(2a+b)x+2(其中x∈[﹣1,a])是偶函數,則實數b=﹣2;
②f(x)= ![]() +
+ ![]() 既是奇函數又是偶函數;
既是奇函數又是偶函數;
③若f(x+2)= ![]() ,當x∈(0,2)時,f(x)=2x , 則f(2015)=2;
,當x∈(0,2)時,f(x)=2x , 則f(2015)=2;
④已知f(x)是定義在R上的不恒為零的函數,且對任意的x,y∈R都滿足f(xy)=xf(y)+yf(x),則f(x)是奇函數.其中所有正確命題的序號是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某數學教師對所任教的兩個班級各抽取20名學生進行測試,分數分布如表:
分數區間 | 甲班頻率 | 乙班頻率 |
[0,30) | 0.1 | 0.2 |
[30,60) | 0.2 | 0.2 |
[60,90) | 0.3 | 0.3 |
[90,120) | 0.2 | 0.2 |
[120,150) | 0.2 | 0.1 |
(Ⅰ)若成績120分以上(含120分)為優秀,求從乙班參加測試的90分以上(含90分)的同學中,隨機任取2名同學,恰有1人為優秀的概率;
(Ⅱ)根據以上數據完成下面的2×2列聯表:在犯錯概率小于0.1的前提下,你是否有足夠的把握認為學生的數學成績是否優秀與班級有關系?
優秀 | 不優秀 | 總計 | |
甲班 | |||
乙班 | |||
總計 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com