
【題目】a,b為空間中兩條互相垂直的直線,等腰直角三角形ABC的直角邊AC所在直線與a,b都垂直,斜邊AB以直線AC為旋轉(zhuǎn)軸旋轉(zhuǎn),有下列結(jié)論:
①當(dāng)直線AB與a成60°角時,AB與b成30°角;
②當(dāng)直線AB與a成60°角時,AB與b成60°角;
③直線AB與a所成角的最小值為45°;
④直線AB與a所成角的最小值為60°;
其中正確的是(填寫所有正確結(jié)論的編號)
【答案】②③
【解析】解:由題意知,a、b、AC三條直線兩兩相互垂直,畫出圖形如圖,
不妨設(shè)圖中所示正方體邊長為1,
故|AC|=1,|AB|= ![]() ,
,
斜邊AB以直線AC為旋轉(zhuǎn)軸,則A點保持不變,
B點的運動軌跡是以C為圓心,1為半徑的圓,
以C坐標原點,以CD為x軸,CB為y軸,CA為z軸,建立空間直角坐標系,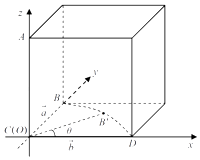
則D(1,0,0),A(0,0,1),直線a的方向單位向量 ![]() =(0,1,0),|
=(0,1,0),| ![]() |=1,
|=1,
直線b的方向單位向量 ![]() =(1,0,0),|
=(1,0,0),| ![]() |=1,
|=1,
設(shè)B點在運動過程中的坐標中的坐標B′(cosθ,sinθ,0),
其中θ為B′C與CD的夾角,θ∈[0,2π),
∴AB′在運動過程中的向量, ![]() =(﹣cosθ,﹣sinθ,1),|
=(﹣cosθ,﹣sinθ,1),| ![]() |=
|= ![]() ,
,
設(shè) ![]() 與
與 ![]() 所成夾角為α∈[0,
所成夾角為α∈[0, ![]() ],
],
則cosα= ![]() =
= ![]() |sinθ|∈[0,
|sinθ|∈[0, ![]() ],
],
∴α∈[ ![]() ,
, ![]() ],∴③正確,④錯誤.
],∴③正確,④錯誤.
設(shè) ![]() 與
與 ![]() 所成夾角為β∈[0,
所成夾角為β∈[0, ![]() ],
],
cosβ= 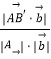 =
= ![]() =
= ![]() |cosθ|,
|cosθ|,
當(dāng) ![]() 與
與 ![]() 夾角為60°時,即α=
夾角為60°時,即α= ![]() ,
,
|sinθ|= ![]() =
= ![]() =
= ![]() ,
,
∵cos2θ+sin2θ=1,∴cosβ= ![]() |cosθ|=
|cosθ|= ![]() ,
,
∵β∈[0, ![]() ],∴β=
],∴β= ![]() ,此時
,此時 ![]() 與
與 ![]() 的夾角為60°,
的夾角為60°,
∴②正確,①錯誤.
故答案為:②③.
由題意知,a、b、AC三條直線兩兩相互垂直,構(gòu)建如圖所示的邊長為1的正方體,|AC|=1,|AB|= ![]() ,斜邊AB以直線AC為旋轉(zhuǎn)軸,則A點保持不變,B點的運動軌跡是以C為圓心,1為半徑的圓,以C坐標原點,以CD為x軸,CB為y軸,CA為z軸,建立空間直角坐標系,利用向量法能求出結(jié)果.
,斜邊AB以直線AC為旋轉(zhuǎn)軸,則A點保持不變,B點的運動軌跡是以C為圓心,1為半徑的圓,以C坐標原點,以CD為x軸,CB為y軸,CA為z軸,建立空間直角坐標系,利用向量法能求出結(jié)果.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() 經(jīng)過
經(jīng)過![]() 兩點,且圓心
兩點,且圓心![]() 在直線
在直線![]() 上.
上.

(1)求圓![]() 的方程;
的方程;
(2)已知過點![]() 的直線
的直線![]() 與圓
與圓![]() 相交截得的弦長為
相交截得的弦長為![]() ,求直線
,求直線![]() 的方程;
的方程;
(3)已知點![]() ,在平面內(nèi)是否存在異于點
,在平面內(nèi)是否存在異于點![]() 的定點
的定點![]() ,對于圓
,對于圓![]() 上的任意動點
上的任意動點![]() ,都有
,都有![]() 為定值?若存在求出定點
為定值?若存在求出定點![]() 的坐標,若不存在說明理由.
的坐標,若不存在說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
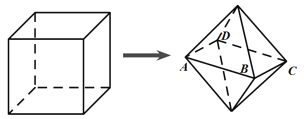
【題目】如圖,棱長為1(單位:![]() )的正方體木塊經(jīng)過適當(dāng)切割,得到幾何體
)的正方體木塊經(jīng)過適當(dāng)切割,得到幾何體![]() ,已知幾何體
,已知幾何體![]() 由兩個底面相同的正四棱錐組成,底面
由兩個底面相同的正四棱錐組成,底面![]() 平行于正方體的下底面,且各頂點均在正方體的面上,則幾何體
平行于正方體的下底面,且各頂點均在正方體的面上,則幾何體![]() 體積的取值范圍是________(單位:
體積的取值范圍是________(單位:![]() ).
).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某人設(shè)計一項單人游戲,規(guī)則如下:先將一棋子放在如圖所示正方形![]() (邊長為2個單位)的頂點
(邊長為2個單位)的頂點![]() 處,然后通過擲骰子來確定棋子沿正方形的邊按逆時針方向行走的單位,如果擲出的點數(shù)為
處,然后通過擲骰子來確定棋子沿正方形的邊按逆時針方向行走的單位,如果擲出的點數(shù)為![]() ,則棋子就按逆時針方向行走
,則棋子就按逆時針方向行走![]() 個單位,一直循環(huán)下去.則某人拋擲三次骰子后棋子恰好又回到點
個單位,一直循環(huán)下去.則某人拋擲三次骰子后棋子恰好又回到點![]() 處的所有不同走法共有( )
處的所有不同走法共有( )

A. 22種 B. 24種 C. 25種 D. 27種
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校學(xué)生參加了“鉛球”和“立定跳遠”兩個科目的體能測試,每個科目的成績分為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五個等級,分別對應(yīng)5分,4分,3分,2分,1分,該校某班學(xué)生兩科目測試成績的數(shù)據(jù)統(tǒng)計如圖所示,其中“鉛球”科目的成績?yōu)?/span>
五個等級,分別對應(yīng)5分,4分,3分,2分,1分,該校某班學(xué)生兩科目測試成績的數(shù)據(jù)統(tǒng)計如圖所示,其中“鉛球”科目的成績?yōu)?/span>![]() 的學(xué)生有8人.
的學(xué)生有8人.

(Ⅰ)求該班學(xué)生中“立定跳遠”科目中成績?yōu)?/span>![]() 的人數(shù);
的人數(shù);
(Ⅱ)若該班共有10人的兩科成績得分之和大于7分,其中有2人10分,3人9分,5人8分.從這10人中隨機抽取兩人,求兩人成績之和![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若橢圓![]() :
:![]() 上有一動點
上有一動點![]() ,
,![]() 到橢圓
到橢圓![]() 的兩焦點
的兩焦點![]() ,
,![]() 的距離之和等于
的距離之和等于![]() ,
,![]() 到直線
到直線![]() 的最大距離為
的最大距離為![]() .
.
(Ⅰ)求橢圓的方程;
(Ⅱ)若過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于不同兩點
交于不同兩點![]() 、
、![]() ,
,![]() (
(![]() 為坐標原點)且
為坐標原點)且![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
在平面直角坐標系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù)),直線
為參數(shù)),直線![]() 與曲線
與曲線![]() :
:![]() 交于
交于![]() ,
,![]() 兩點.
兩點.
(Ⅰ)求![]() 的長;
的長;
(Ⅱ)在以![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立的極坐標系中,設(shè)點
軸的正半軸為極軸建立的極坐標系中,設(shè)點![]() 的極坐標為
的極坐標為![]() ,求點
,求點![]() 到線段
到線段![]() 中點
中點![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓的中心在坐標原點![]() ,焦點在
,焦點在![]() 軸上,短軸長為
軸上,短軸長為![]() ,且兩個焦點和短軸的兩個端點恰為一個正方形的頂點.
,且兩個焦點和短軸的兩個端點恰為一個正方形的頂點.
(1)求橢圓的方程;
(2)設(shè)過右焦點![]() 與
與![]() 軸不垂直的直線與橢圓交于
軸不垂直的直線與橢圓交于![]() 、
、![]() 兩點.在線段
兩點.在線段![]() 上是否存在點
上是否存在點![]() ,使得以
,使得以![]() 、
、![]() 為鄰邊的平行四邊形是菱形?若存在,求出
為鄰邊的平行四邊形是菱形?若存在,求出![]() 的取值范圍;若不存在,
的取值范圍;若不存在,
請說明理由;
(3)設(shè)點![]() 在橢圓上運動,
在橢圓上運動,![]() ,且點
,且點![]() 到直線
到直線![]() 的距離等于
的距離等于![]() ,試求動點
,試求動點![]() 的軌
的軌
跡方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若二次函數(shù)f(x)=ax2+bx+c(a≠0)的圖象與直線y=x無交點,現(xiàn)有下列結(jié)論:
①若a=1,b=2,則c>![]()
②若a+b+c=0,則不等式f(x)>x對一切實數(shù)x都成立
③函數(shù)g(x)=ax2﹣bx+c的圖象與直線y=﹣x也一定沒有交點
④若a>0,則不等式f[f(x)]>x對一切實數(shù)x都成立
⑤方程f[f(x)]=x一定沒有實數(shù)根
其中正確的結(jié)論是 (寫出所有正確結(jié)論的編號)
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com