
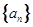 中,
中,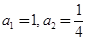 ,且
,且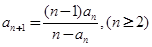 .
.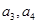 ,猜想
,猜想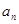 的表達式,并加以證明;
的表達式,并加以證明;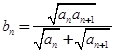 ,求證:對任意的自然數
,求證:對任意的自然數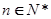 ,都有
,都有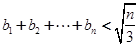 ;
;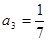 ,
,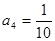 ;
; ,
,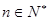 證明:見解析.
證明:見解析.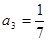 ,
,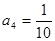 ----------------------(2分)
----------------------(2分) ,
,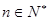 下面利用數學歸納法加以證明:
下面利用數學歸納法加以證明: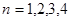 時,結論成立,-----------------(3分)
時,結論成立,-----------------(3分)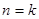 ;
; 時(也可以
時(也可以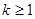 ),結論也成立,即
),結論也成立,即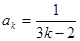 ,
,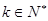 --------------------------(4分)
--------------------------(4分)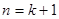 時,由題設與歸納假設可知:
時,由題設與歸納假設可知: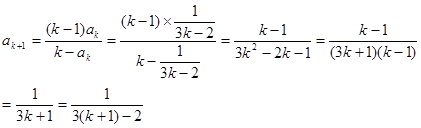 ------------(6分)
------------(6分)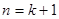 時,結論也成立,綜上,對
時,結論也成立,綜上,對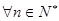 ,
, 成立。--------(7分)
成立。--------(7分)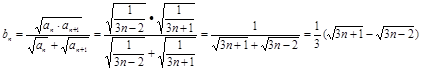 ---(9分)
---(9分)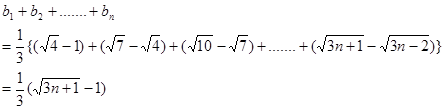 ---------(11分)
---------(11分)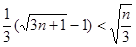
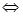
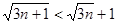
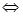
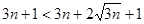
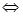
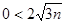 (顯然成立)
(顯然成立)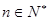 ,都有
,都有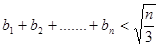 -------(14分)
-------(14分)

 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:不詳 題型:填空題
 是等和數列,
是等和數列, =3,公和是5,則此數列的前805項的和為 .
=3,公和是5,則此數列的前805項的和為 .查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| A.5 | B.6 | C.7 | D.8 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com