
為了加快經濟的發展,某省選擇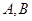 兩城市作為龍頭帶動周邊城市的發展,決定在
兩城市作為龍頭帶動周邊城市的發展,決定在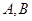 兩城市的周邊修建城際輕軌,假設
兩城市的周邊修建城際輕軌,假設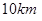 為一個單位距離,
為一個單位距離,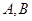 兩城市相距
兩城市相距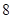 個單位距離,設城際輕軌所在的曲線為
個單位距離,設城際輕軌所在的曲線為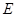 ,使輕軌
,使輕軌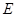 上的點到
上的點到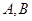 兩城市的距離之和為
兩城市的距離之和為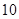 個單位距離,
個單位距離,
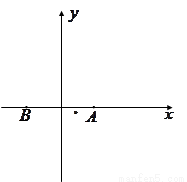
(1)建立如圖的直角坐標系,求城際輕軌所在曲線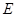 的方程;
的方程;
(2)若要在曲線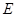 上建一個加油站
上建一個加油站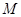 與一個收費站
與一個收費站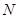 ,使
,使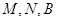 三點在一條直線上,并且
三點在一條直線上,并且 個單位距離,求
個單位距離,求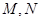 之間的距離有多少個單位距離?
之間的距離有多少個單位距離?
(3)在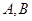 兩城市之間有一條與
兩城市之間有一條與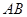 所在直線成
所在直線成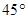 的筆直公路
的筆直公路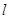 ,直線
,直線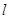 與曲線
與曲線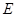 交于
交于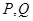 兩點,求四邊形
兩點,求四邊形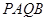 的面積的最大值.
的面積的最大值.
(1)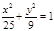 (2)8(3)
(2)8(3)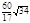
【解析】(1)根據題目條件選取適當的坐標系,本小題應該以AB所在直線為x軸,AB的垂直平分線為y軸建立直角坐標系,這樣得到的軌跡方程是標準方程,有利于下一步的計算.
(2)由橢圓的定義可知|AM|+|AN|+|BM|+|BN|=20,|AM|+|AN|=12,所以|MN|=8.
(3)先求出四邊形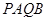 的面積的表達式,設直線方程為y=x+t,然后與橢圓方程聯立,消x后得到關于y的一元二次方程,借助韋達定理,根據
的面積的表達式,設直線方程為y=x+t,然后與橢圓方程聯立,消x后得到關于y的一元二次方程,借助韋達定理,根據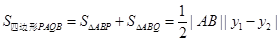 ,
,
求出面積關于t的函數表達式,利用函數的方法求最值即可.
解:(1)以AB為x軸,以AB中點為原點O建立直角坐標系,設曲線E上點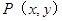 ,
,
∵|PA|+|PB|=10>|AB|=8
∴動點軌跡為橢圓,且a=5,c=4,從面b=3.
∴曲線E的方程為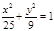 4分
4分
(2)由|AM|+|AN|+|BM|+|BN|=20,|AM|+|AN|=12,所以|MN|=8 8分
(3)將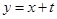 代入
代入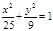 ,得
,得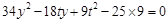
設
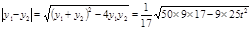
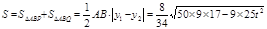
所以當t=0時,面積最大是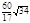 ,此時直線為l:y=x 13分
,此時直線為l:y=x 13分


 王后雄學案教材完全解讀系列答案
王后雄學案教材完全解讀系列答案 海淀課時新作業金榜卷系列答案
海淀課時新作業金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:2011-2012學年福建省高三5月模擬考試文科數學試卷(解析版) 題型:解答題
(本小題滿分12分)
為了加快經濟的發展,某市選擇A、B兩區作為龍頭帶動周邊地區的發展,決定在A、B兩區的周邊修建城際快速通道,假設A、B兩區相距 個單位距離,城際快速通道所在的曲線為E,使快速通道E上的點到兩區的距離之和為4個單位距離.
個單位距離,城際快速通道所在的曲線為E,使快速通道E上的點到兩區的距離之和為4個單位距離.

(Ⅰ)以線段AB的中點O為原點建立如圖所示的直角坐標系,求城際快速通道所在曲線E的方程;
(Ⅱ)若有一條斜率為 的筆直公路l與曲線E交于P,Q兩點,同時在曲線E上建一個加油站M(橫坐標為負值)滿足
的筆直公路l與曲線E交于P,Q兩點,同時在曲線E上建一個加油站M(橫坐標為負值)滿足 ,求
,求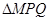 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源:藍山縣模擬 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com