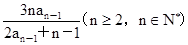已知函數
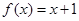
,設
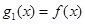
,
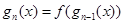
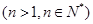
.
(1)猜測并直接寫出
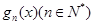
的表達式;此時若設
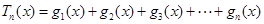
,且關于
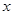
的函數
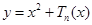
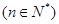
在區間
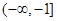
上的最小值為
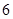
,則求
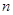
的值;
(2)設數列
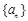
為等比數列,數列
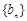
滿足
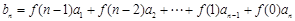
,
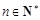
,若
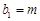
,
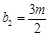
,其中
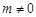
,則
①當
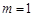
時,求
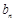
;
②設
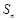
為數列
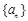
的前
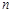
項和,若對于任意的正整數
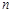
,都有
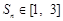
,求實數
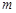
的取值范圍.
①
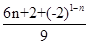
②
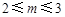
(I)先分別求出
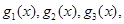
從而歸納出
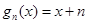
,所以
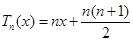
.這樣可得到
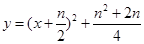
.
然后再討論二次函數的對稱軸
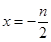
與-1的大小關系即可.
(2)在(1)的基礎上,可得
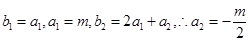
,所以數列
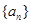
的公比為
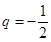
,當m=1時,
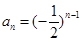
,所以
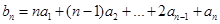
,
所以
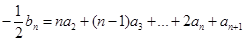
,然后兩式作差整理可得
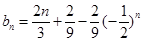
,問題到此基本得以解決.
解:(1)∵
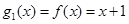
,
∴
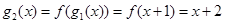
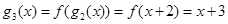
.…1分
∴
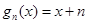
.………………2分
∴
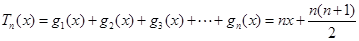
.
∴
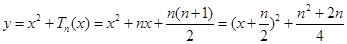
.…………4分
ⅰ)當
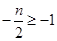
,即
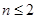
時,函數
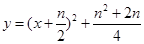
在區間
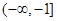
上是減函數,
∴當
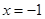
時,
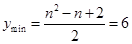
,即

,該方程沒有整數解.…5分
ⅱ)當
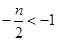
,即
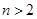
時,

,解得
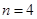
,綜上所述,
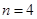
.…6分;
(2)①由已知
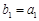
,所以
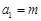
;
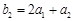
,所以
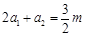
,解得
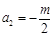
; 所以數列
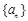
的公比
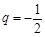
; ....7分當
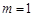
時,
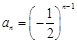
,
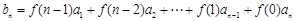
,即
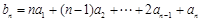
…①
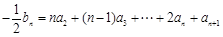
,………②,
②-①得
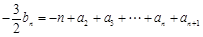
,
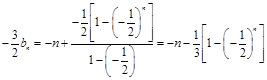
,....8分
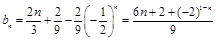
.....9分
②
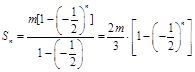
.....10分
因為
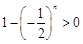
,所以由
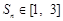
得
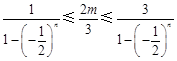
,....11分
注意到,當n為奇數時,

;
當
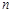
為偶數時,
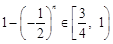
,
所以
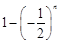
最大值為
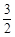
,最小值為
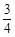
.....13分
對于任意的正整數n都有
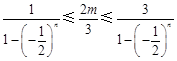
,
所以

,解得
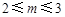
...14分
練習冊系列答案
相關習題
科目:高中數學
來源:不詳
題型:解答題
已知定義在R上的函數
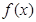
和數列
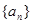
滿足下列條件:
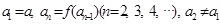
,
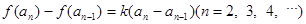
,其中a為常數,k為非零常數.
(Ⅰ)令
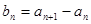
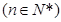
,證明數列
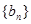
是等比數列;
(Ⅱ)求數列
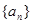
的通項公式;
(Ⅲ)當
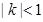
時,求
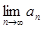
.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
已知數列
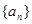
中各項均為正數,
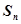
是數列
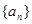
的前
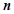
項和,且
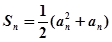
.
(1)求數列
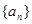
的通項公式
(2)對
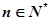
,試比較
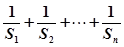
與
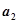
的大小.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
已知數列{a
n}滿足:a
1=
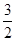
,且a
n=
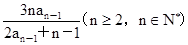
(1) 求數列{a
n}的通項公式;
(2) 證明:對于一切正整數n,不等式a
1·a
2·……a
n<2·n!
查看答案和解析>>
科目:高中數學
來源:不詳
題型:單選題
若兩等差數列
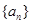
、
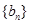
前
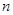
項和分別為
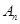
、
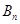
,滿足
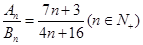
,
則
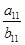
的值為( )
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
.(本小題滿分12分) 已知等差數列
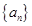
滿足:

,
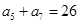
,
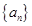
的前
n項和為
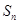
.
(Ⅰ)求通項公式
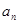
及前
n項和
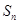
;
(Ⅱ)令
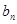
=
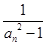
(
n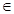
N
*),求數列
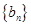
的前
n項和
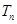
.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:單選題
在等差數列
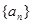
中,
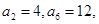
則公差d= ( )
查看答案和解析>>
主站蜘蛛池模板:
韩国毛片在线观看
|
久草成人网
|
久久成人综合
|
中文字幕色站
|
亚洲精品自拍
|
黄色一级视|
亚洲 欧美 综合
|
欧美成人综合视频
|
欧美成人精品一区二区男人看
|
热re99久久精品国99热线看
|
欧美日一区二区
|
成人免费淫片aa视频免费
|
亚洲免费黄色
|
国产亚洲精品精品国产亚洲综合
|
久久精品一级
|
亚洲九九
|
亚洲欧美日韩另类精品一区二区三区
|
呦一呦二在线精品视频
|
久久精品一
|
国产亚洲成av人片在线观看
|
日韩精品一区二区三区免费视频
|
国产精品美女视频免费观看软件
|
天天干夜夜骑
|
欧美激情精品久久久久久
|
精品国产欧美一区二区三区成人
|
伊人久操
|
亚洲高清在线观看
|
福利二区视频
|
久久久www成人免费精品
|
一区二区三区视频免费在线观看
|
久久久久久久久久97
|
91在线免费看
|
91佛爷在线观看
|
日韩一区二区福利
|
欧美日本在线播放
|
亚洲精品久久一区二区三区
|
精品久久久久一区二区三区
|
欧洲色
|
久久这里只有精品首页
|
亚洲 欧美 激情 另类 校园
|
韩国xxxx性hd极品
|

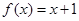 ,設
,設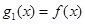 ,
,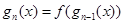
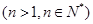 .
. 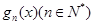 的表達式;此時若設
的表達式;此時若設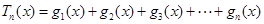 ,且關于
,且關于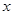 的函數
的函數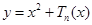
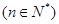 在區間
在區間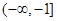 上的最小值為
上的最小值為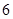 ,則求
,則求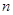 的值;
的值;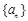 為等比數列,數列
為等比數列,數列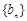 滿足
滿足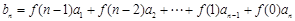 ,
,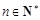 ,若
,若 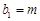 ,
,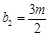 ,其中
,其中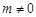 ,則
,則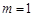 時,求
時,求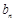 ;
;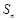 為數列
為數列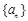 的前
的前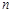 項和,若對于任意的正整數
項和,若對于任意的正整數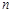 ,都有
,都有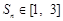 ,求實數
,求實數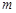 的取值范圍.
的取值范圍.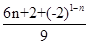 ②
②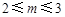
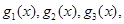 從而歸納出
從而歸納出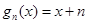 ,所以
,所以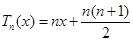 .這樣可得到
.這樣可得到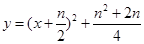 .
.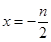 與-1的大小關系即可.
與-1的大小關系即可.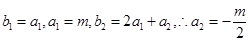 ,所以數列
,所以數列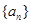 的公比為
的公比為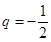 ,當m=1時,
,當m=1時,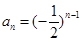 ,所以
,所以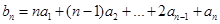 ,
,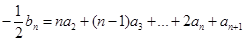 ,然后兩式作差整理可得
,然后兩式作差整理可得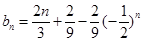 ,問題到此基本得以解決.
,問題到此基本得以解決.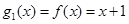 ,
,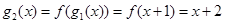
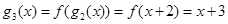 .…1分
.…1分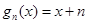 .………………2分
.………………2分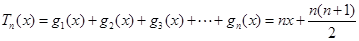 .
. 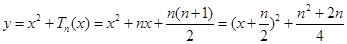 .…………4分
.…………4分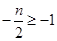 ,即
,即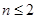 時,函數
時,函數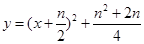 在區間
在區間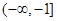 上是減函數,
上是減函數,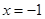 時,
時,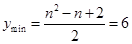 ,即
,即 ,該方程沒有整數解.…5分
,該方程沒有整數解.…5分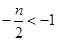 ,即
,即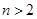 時,
時, ,解得
,解得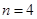 ,綜上所述,
,綜上所述,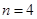 .…6分;
.…6分;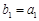 ,所以
,所以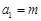 ;
;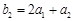 ,所以
,所以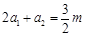 ,解得
,解得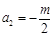 ; 所以數列
; 所以數列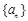 的公比
的公比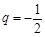 ; ....7分當
; ....7分當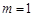 時,
時,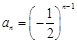 ,
,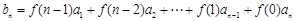 ,即
,即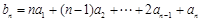 …①
…① 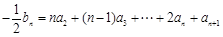 ,………②,
,………②, 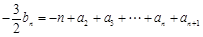 ,
,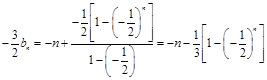 ,....8分
,....8分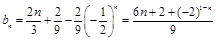 .....9分
.....9分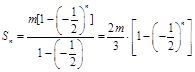 .....10分
.....10分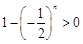 ,所以由
,所以由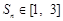 得
得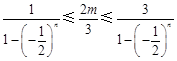 ,....11分
,....11分 ;
; 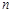 為偶數時,
為偶數時,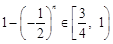 ,
,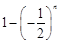 最大值為
最大值為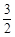 ,最小值為
,最小值為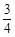 .....13分
.....13分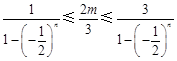 ,
, ,解得
,解得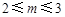 ...14分
...14分

 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案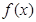 和數列
和數列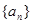 滿足下列條件:
滿足下列條件: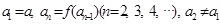 ,
,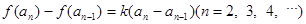 ,其中a為常數,k為非零常數.
,其中a為常數,k為非零常數.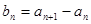
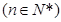 ,證明數列
,證明數列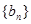 是等比數列;
是等比數列;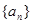 的通項公式;
的通項公式;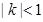 時,求
時,求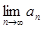 .
.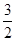 ,且an=
,且an=