Question

（1）已知Z是復數，求證：①；②；
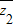（2）已知z₁，z₂是復數，若|z₁-|=|1-z₁z₂|，求證：|z₁|，|z₂|中至少有一個值為1．

Answer 1

【答案】分析：（1）設 z=a+bi，a、b∈R，分別代入兩個等式的左右兩邊化簡，即可證得等式成立．
（2）把已知條件兩邊平方，利用共軛復數的性質化簡可得z₁+z₂=1+z₁z₂ ，可得（|z₁|²-1）（|z₂|²-1）
=0，從而有|z₁|，|z₂|中至少有一個為1．
解答：解：（1）設 z=a+bi，a、b∈R，
∵|Z|²=a²+b²，=9a+bi）（a-bi）=a²+b²，∴① 成立．
∵==-2bi，=（a-bi）-（a+bi）=-2bi，∴②成立．
（2）∵|z₁-|=|1-z₁z₂|，∴|z₁-|² =|1-z₁z₂|² ．
∴（z₁-） （ ）=（1-z₁z₂）（1- ）．
∴（z₁-）（-z₂）=（ 1-z₁z₂）（1-）．
化簡后得z₁+z₂=1+z₁z₂ ．
∴|z₁|²+|z₂|²=1+|z₁|²•|z₂|²．∴（|z₁|²-1）（|z₂|²-1）=0．
∴|z₁|²=1，或|z₂|²=1．∴|z₁|，|z₂|中至少有一個為1．
點評：本題主要考查共軛復數的定義和性質，兩個復數代數形式的乘除法，求復數的模的方法，屬于基礎題．