Question

（2014•江門模擬）平面直角坐標系中，拋物線y2=

1

2

x與函數y=lnx圖象的交點個數為（　　）

A．0

B．1

C．2

D．3

Answer 1

分析：顯然，拋物線y2=

1

2

x與函數y=lnx圖象在第四象限內有一個交點，其它交點只能在第一象限內．令f（x）=

2

2

•

x

-lnx （x＞0），利用導數求得f（x）在（0，+∞）上有兩個零點，可得拋物線y2=

1

2

x與函數y=lnx圖象在第一象限內有2個交點，綜合可得結論．

解答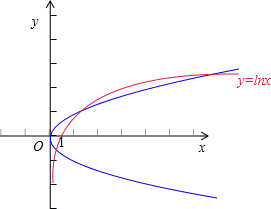：解：顯然，拋物線y2=

1

2

x與函數y=lnx圖象在
第四象限內有一個交點．
其它交點只能在第一象限內，在第一象限內，
拋物線方程為y=

2

2

x．
令f（x）=

2

2

•

x

-lnx （x＞0），
則f′（x）=

2

4

•

1

x

-

1

x

=

2x -4

4x

，
令f′（x）=0，求得x=8．
在（0，8）上，f′（x）＜0，f（x）為減函數；
在（8，+∞）上，f′（x）＞0，f（x）為增函數，
故f（8）為函數f（x）的極小值，且f（8）=2-ln8＜0．
再根據f（1）＞0，且當x足夠大時，f（x）＞0，
故函數f（x）在（0，+∞）上有2個零點，
即拋物線y2=

1

2

x與函數y=lnx圖象在第一象限內有2個交點（如圖所示）．
綜上可得，拋物線y2=

1

2

x與函數y=lnx圖象有3個交點，
故答案為 3．

點評：本題主要考查方程根的存在性及個數判斷，體現了轉化以及數形結合的數學思想，屬于中檔題．