
【題目】設圓![]() 的圓心為
的圓心為![]() ,直線
,直線![]() 過點
過點![]() 且不與
且不與![]() 軸、
軸、![]() 軸垂直,且與圓
軸垂直,且與圓![]() 于
于![]() ,
, ![]() 兩點,過
兩點,過![]() 作
作![]() 的平行線交直線
的平行線交直線![]() 于點
于點![]() .
.
(1)證明![]() 為定值,并寫出點
為定值,并寫出點![]() 的軌跡方程;
的軌跡方程;
(2)設點![]() 的軌跡為曲線
的軌跡為曲線![]() ,直線
,直線![]() 交
交![]() 于
于![]() 兩點,過
兩點,過![]() 且與
且與![]() 垂直的直線與圓
垂直的直線與圓![]() 交于
交于![]() 兩點,求
兩點,求![]() 與
與![]() 的面積之和的取值范圍.
的面積之和的取值范圍.
【答案】(1)![]() .(2)
.(2)![]()
【解析】試題分析:(1)先證明![]() ,可得,
,可得, ![]() ,進而得
,進而得![]() ,由雙曲線定義知軌跡是雙曲線,從而可得方程;(2)聯立直線
,由雙曲線定義知軌跡是雙曲線,從而可得方程;(2)聯立直線![]() 與雙曲線
與雙曲線![]() 的方程
的方程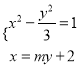 ,消去
,消去![]() 得
得![]() ,根據弦長公式、點到直線距離公式及三角形面積公式可得三角形面積之和成關于
,根據弦長公式、點到直線距離公式及三角形面積公式可得三角形面積之和成關于![]() 的函數,利用單調心求解即可.
的函數,利用單調心求解即可.
試題解析:(1)
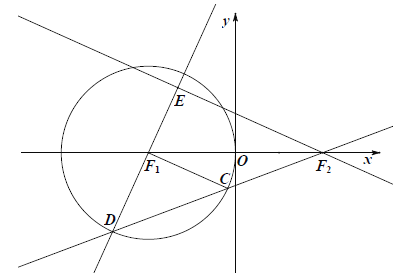
圓![]() ,圓心
,圓心![]() ,半徑
,半徑![]() ,如圖所示.
,如圖所示.
因為![]() ,所以
,所以![]() .又因為
.又因為![]() ,所以
,所以![]() ,
,
所以![]() ,
,
又因為![]() ,所以
,所以![]() ,
,
故![]() ,可得
,可得![]() ,
,
根據雙曲線的定義,可知點![]() 的軌跡是以
的軌跡是以![]() 為焦點的雙曲線(頂點除外),
為焦點的雙曲線(頂點除外),
易得點![]() 的軌跡方程為
的軌跡方程為![]() .
.
(2)![]() .
.
依題意可設![]() ,
,
由于![]() ,設
,設![]() .
.
圓心![]() 到直線
到直線![]() 的距離
的距離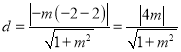 ,
,
所以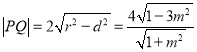 ,
,
又因為![]() ,解得
,解得![]() .
.
聯立直線![]() 與雙曲線
與雙曲線![]() 的方程
的方程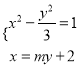 ,消去
,消去![]() 得
得![]() ,
,
則![]() ,
,
所以![]() ,
,
記![]() 的面積分別為
的面積分別為![]() ,
,
則 ,
,
又因為![]() ,所以
,所以![]() ,
,
所以![]() 的取值范圍為
的取值范圍為![]() .
.
【方法點晴】本題主要考查待定系數法求橢圓方程及圓錐曲線求最值,屬于難題.解決圓錐曲線中的最值問題一般有兩種方法:一是幾何意義,特別是用圓錐曲線的定義和平面幾何的有關結論來解決,非常巧妙;二是將圓錐曲線中最值問題轉化為函數問題,然后根據函數的特征選用參數法、配方法、判別式法、三角函數有界法、函數單調性法以及均值不等式法,本題(2)就是用的這種思路,利用單調性法法求三角形三角形面積之和的最值的.


 步步高口算題卡系列答案
步步高口算題卡系列答案 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:高中數學 來源: 題型:
【題目】為了響應教育部頒布的《關于推進中小學生研學旅行的意見》,某校計劃開設八門研學旅行課程,并對全校學生的選擇意向進行調查(調查要求全員參與,每個學生必須從八門課程中選出唯一一門課程).本次調查結果整理成條形圖如下.

上圖中,已知課程![]() 為人文類課程,課程
為人文類課程,課程![]() 為自然科學類課程.為進一步研究學生選課意向,結合上面圖表,采取分層抽樣方法從全校抽取
為自然科學類課程.為進一步研究學生選課意向,結合上面圖表,采取分層抽樣方法從全校抽取![]() 的學生作為研究樣本組(以下簡稱“組M”).
的學生作為研究樣本組(以下簡稱“組M”).
(Ⅰ)在“組M”中,選擇人文類課程和自然科學類課程的人數各有多少?
(Ⅱ)為參加某地舉辦的自然科學營活動,從“組M”所有選擇自然科學類課程的同學中隨機抽取4名同學前往,其中選擇課程F或課程H的同學參加本次活動,費用為每人1500元,選擇課程G的同學參加,費用為每人2000元.
(ⅰ)設隨機變量![]() 表示選出的4名同學中選擇課程
表示選出的4名同學中選擇課程![]() 的人數,求隨機變量
的人數,求隨機變量![]() 的分布列;
的分布列;
(ⅱ)設隨機變量![]() 表示選出的4名同學參加科學營的費用總和,求隨機變量
表示選出的4名同學參加科學營的費用總和,求隨機變量![]() 的期望.
的期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+α)(A>0,ω>0,﹣ ![]() <α<
<α< ![]() )的最小正周期是π,且當x=
)的最小正周期是π,且當x= ![]() 時,f(x)取得最大值2.
時,f(x)取得最大值2.
(1)求f(x)的解析式,并作出f(x)在[0,π]上的圖象(要列表);
(2)將函數f(x)的圖象向右平移m(m>0)個單位長度后得到函數y=g(x)的圖象,且y=g(x)是偶函數,求m的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班級有50名學生,其中有30名男生和20名女生,隨機詢問了該班五名男生和五名女生在某次數學測驗中的成績,五名男生的成績分別為86,94,88,92,90,五名女生的成績分別為88,93,93,88,93,下列說法正確的是( )
A.這種抽樣方法是一種分層抽樣
B.這種抽樣方法是一種系統抽樣
C.這五名男生成績的方差大于這五名女生成績的方差
D.該班男生成績的平均數大于該班女生成績的平均數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若關于x的不等式(a2﹣a)4x﹣2x﹣1<0在區間(﹣∞,1]上恒成立,則實數a的取值范圍為( )
A.(﹣2, ![]() )
)
B.(﹣∞, ![]() )
)
C.(﹣ ![]() ,
, ![]() )
)
D.(﹣∞,6]
查看答案和解析>>
科目:高中數學 來源: 題型:
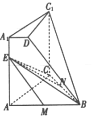
【題目】如圖,幾何體![]() 由一個正三棱柱截去一個三棱錐而得,
由一個正三棱柱截去一個三棱錐而得, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() 為
為![]() 的中點,
的中點, ![]() 為棱
為棱![]() 上一點,且
上一點,且![]() 平面
平面![]() .
.
(1)若![]() 在棱
在棱![]() 上,且
上,且![]() ,證明:
,證明: ![]() 平面
平面![]() ;
;
(2)過![]() 作平面
作平面![]() 的垂線,垂足為
的垂線,垂足為![]() ,確定
,確定![]() 的位置(說明作法及理由),并求線段
的位置(說明作法及理由),并求線段![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com