(理科做)某城市有甲、乙、丙3個旅游景點,一位客人游覽這三個景點的概率分別是0.4,0.5,0.6,且客人是否游覽哪個景點互不影響,設ξ表示客人離開該城市時游覽的景點數與沒有游覽的景點數之差的絕對值.
(Ⅰ)求ξ的分布及數學期望;
(Ⅱ)記“函數f(x)=x2-3ξx+1在區間[2,+∞)上單調遞增”為事件A,求事件A的概率.
【答案】
分析:(I)ξ表示客人離開該城市時游覽的景點數與沒有游覽的景點數之差的絕對值,根據客人游覽的景點數的可能取值為0,1,2,3.和客人沒有游覽的景點數的可能取值為3,2,1,0,寫出變量的可能取值,根據相互獨立事件同時發生的概率寫出分布列和期望.
(II)由題意知本題是一個等可能事件的概率,函數f(x)=x
2-3ξx+1在區間[2,+∞)上單調遞增,根據二次函數的性質,寫出函數遞增的變量的值,知道只有當變量對應1是成立,得到結果.
解答:解:(I)分別記“客人游覽甲景點”,“客人游覽乙景點”,“客人游覽丙景點”
為事件A
1,A
2,A
3.由已知A
1,A
2,A
3相互獨立,P(A
1)=0.4,P(A
2)=0.5,P(A
3)=0.6.
客人游覽的景點數的可能取值為0,1,2,3.相應地,客人沒有游覽的景點數的可能取值為3,2,1,0,所以ξ的可能取值為1,3.
P(ξ=3)=P(A
1•A
2•A
3)+P(
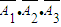
)
=P(A
1)P(A
2)P(A
3)+P(
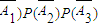
)
=2×0.4×0.5×0.6=0.24,
P(ξ=1)=1-0.24=0.76.
所以ξ的分布列為
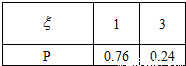
Eξ=1×0.76+3×0.24=1.48.
(Ⅱ)因為
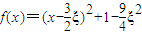
,
所以函數
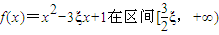
上單調遞增,
要使f(x)在[2,+∞)上單調遞增,當且僅當

.
從而

.
點評:本題考查離散型隨機變量的分布列和期望,考查等可能事件的概率,考查二次函數的性質,是一個綜合題目,這種題目可以作為解答題目出現在高考試卷中.

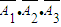 )
)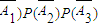 )
)
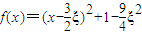 ,
,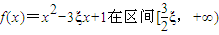 上單調遞增,
上單調遞增, .
. .
.
