Question

在由數字1，2，3，4，5組成的所有沒有重復數字的5位數中，大于23145且小于43521的數共有    種．

Answer 1

【答案】分析：本題是一個分類計數問題，用1、2、3、4、5組成無重復五位數，大于23145且小于43521的，可以通過分類做出所有的情況，再用分類計數原理得到結果．
解答：解：由題意知本題是一個分類計數問題，
1、2、3、4、5組成無重復五位數，大于23145且小于43521的有
形如，后兩位只能填5、4，
∴有1種數合要求．
形如25---，第三位選4或5都滿足要求，后兩位任選都可．
∴符合要求的數有C₂¹•A₂²=4種．
形如，第二位選4或5，后三位任選，
∴方法數為C₂¹•A₃³=12種．
形如3----，第二位開始，均可任選
∴方法數為A₄⁴=24種．
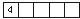
形如，第二位選1或2，后三位任選，
方法數為C₂¹•A₃³=12種．
同理形如，2A₂²=4種，
形如，1種．
∴合要求總數為（1+4+12）×2+24=58種．
故答案為：58．
點評：本題考查分類計數原理，考查通過不重不漏的列舉出滿足條件的事件寫出結果數，這種問題比較麻煩，計算時容易出錯，需要認真的做出來