
已知橢圓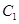 的中心在坐標原點,兩個焦點分別為
的中心在坐標原點,兩個焦點分別為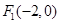 ,
,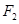
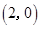 ,點
,點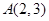 在橢圓
在橢圓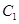 上,過點
上,過點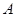 的直線
的直線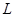 與拋物線
與拋物線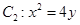 交于
交于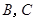 兩點,拋物線
兩點,拋物線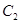 在點
在點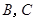 處的切線分別為
處的切線分別為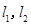 ,且
,且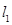 與
與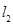 交于點
交于點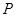 .
.
(1) 求橢圓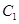 的方程;
的方程;
(2) 是否存在滿足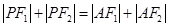 的點
的點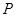 ? 若存在,指出這樣的點
? 若存在,指出這樣的點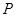 有幾個(不必求出點
有幾個(不必求出點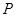 的坐標); 若不存在,說明理由.
的坐標); 若不存在,說明理由.
(1)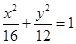 .
(2)滿足條件的點
.
(2)滿足條件的點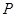 有兩個.
有兩個.
【解析】
(1)試題分析:解法1:設橢圓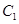 的方程為
的方程為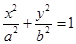
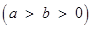 ,依題意:
,依題意: 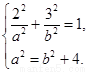
解得: 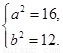 ∴ 橢圓
∴ 橢圓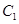 的方程為
的方程為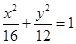 .
.
解法2:設橢圓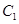 的方程為
的方程為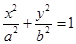
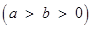 ,根據橢圓的定義得
,根據橢圓的定義得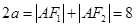 ,即
,即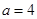 , ∵
, ∵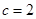 , ∴
, ∴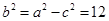 . ∴ 橢圓
. ∴ 橢圓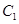 的方程為
的方程為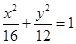 .
.
(2) 解法1:顯然直線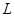 的斜率存在,設直線
的斜率存在,設直線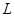 的方程為
的方程為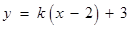 ,
,
由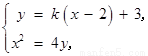 消去
消去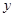 ,得
,得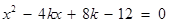 .
.
設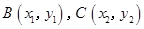 ,則
,則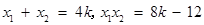 .
.
由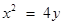 ,即
,即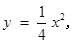 得
得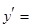
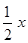 .
.
∴拋物線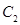 在點
在點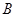 處的切線
處的切線 的方程為
的方程為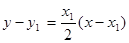 ,即
,即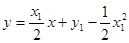 .
.
∵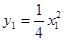 , ∴
, ∴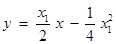 .
.
同理,得拋物線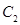 在點
在點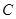 處的切線
處的切線 的方程為
的方程為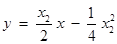 .
.
由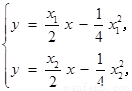 解得
解得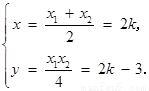
∴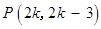 . ∵
. ∵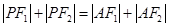 ,
,
∴點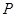 在橢圓
在橢圓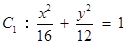 上. ∴
上. ∴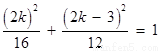 .
.
化簡得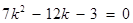 .(*) 由
.(*) 由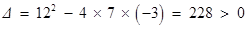 ,
,
可得方程(*)有兩個不等的實數根. ∴滿足條件的點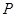 有兩個.
有兩個.
解法2:設點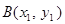 ,
,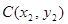 ,
,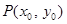 ,由
,由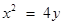 ,即
,即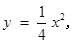 得
得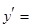
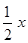 .
.
∴拋物線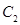 在點
在點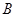 處的切線
處的切線 的方程為
的方程為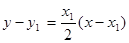 ,
,
即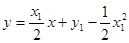 .∵
.∵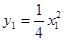 , ∴
, ∴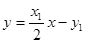 .
.
∵點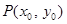 在切線
在切線 上, ∴
上, ∴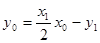 . ①
. ①
同理, 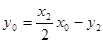 . ② 綜合①、②得,點
. ② 綜合①、②得,點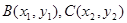 的坐標都滿足方程
的坐標都滿足方程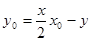 .∵經過
.∵經過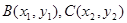 的直線是唯一的,∴直線
的直線是唯一的,∴直線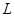 的方程為
的方程為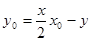 ,
,
∵點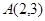 在直線
在直線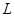 上, ∴
上, ∴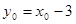 . ∴點
. ∴點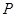 的軌跡方程為
的軌跡方程為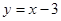 .
.
若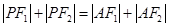 ,則點
,則點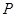 在橢圓
在橢圓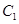 上,又在直線
上,又在直線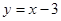 上,∵直線
上,∵直線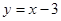 經過橢圓
經過橢圓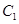 內一點
內一點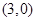 ,∴直線
,∴直線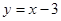 與橢圓
與橢圓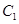 交于兩點.
交于兩點.
∴滿足條件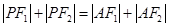 的點
的點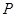 有兩個.
有兩個.
解法3:設點 ,
,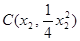 ,則
,則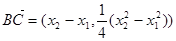 ,
,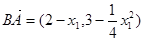 ,
,
∵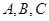 三點共線,
三點共線,  .
. 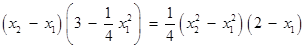
化簡得: . ① 由
. ① 由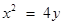 ,即
,即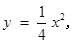 得
得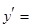
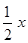 .
.
∴拋物線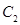 在點
在點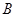 處的切線
處的切線 的方程為
的方程為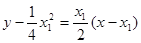 ,即
,即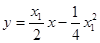 . ②
. ②
同理,拋物線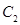 在點
在點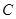 處的切線
處的切線 的方程為
的方程為 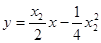 . ③
. ③
設點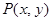 ,由②③得:
,由②③得: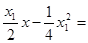
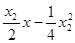 ,而
,而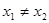 ,則
,則 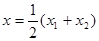 .
.
代入②得
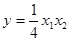 , 則
, 則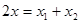 ,
, 代入 ① 得
代入 ① 得
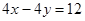 ,
,
即點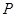 的軌跡方程為
的軌跡方程為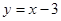 .若
.若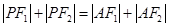 ,則點
,則點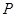 在橢圓
在橢圓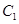 上,而點
上,而點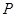 又在直線
又在直線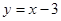 上,∵直線
上,∵直線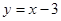 經過橢圓
經過橢圓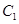 內一點
內一點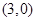 ,
,
∴直線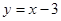 與橢圓
與橢圓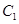 交于兩點. ∴滿足條件
交于兩點. ∴滿足條件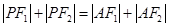 的點
的點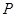 有兩個.
有兩個.
考點:本題考查了圓錐曲線的方程及直線與圓錐曲線的位置關系
點評:解答此類問題時注意若直線與圓錐曲線有兩個交點,對待交點坐標是“設而不求”的原則,要注意應用韋達定理處理這類問題


 暑假作業海燕出版社系列答案
暑假作業海燕出版社系列答案 本土教輔贏在暑假高效假期總復習云南科技出版社系列答案
本土教輔贏在暑假高效假期總復習云南科技出版社系列答案 暑假作業北京藝術與科學電子出版社系列答案
暑假作業北京藝術與科學電子出版社系列答案科目:高中數學 來源: 題型:
 已知橢圓的中心在坐標原點O,焦點在x軸上,短軸長為2,且兩個焦點和短軸的兩個端點恰為一個正方形的頂點.過右焦點F與x軸不垂直的直線l交橢圓于P,Q兩點.
已知橢圓的中心在坐標原點O,焦點在x軸上,短軸長為2,且兩個焦點和短軸的兩個端點恰為一個正方形的頂點.過右焦點F與x軸不垂直的直線l交橢圓于P,Q兩點.查看答案和解析>>
科目:高中數學 來源: 題型:
2
| ||
| 5 |
| ||
| 5 |
| AC |
| AO |
| AC |
| AO |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 3 |
| x2 |
| 36 |
| y2 |
| 9 |
| x2 |
| 36 |
| y2 |
| 9 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| ||
| 2 |
| ||
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com