
如圖,直線 過圓心
過圓心 ,交⊙
,交⊙ 于
于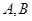 ,直線
,直線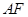 交⊙
交⊙ 于
于 (不與
(不與 重合),直線
重合),直線 與⊙
與⊙ 相切于
相切于 ,交
,交 于
于 ,且與
,且與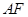 垂直,垂足為
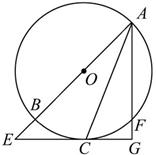
垂直,垂足為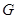 ,連結(jié)
,連結(jié)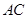 .
.
求證:(1)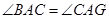 ;
;
(2)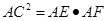 .
.
(1)利用弦切角∠BAC=∠CAG.(2)利用三角形相似。 AC2=AE·AF.
解析試題分析:(1)連結(jié)BC,∵AB是直徑,
∴∠ACB=90°,∴∠ACB=∠AGC=90°.
∵GC切⊙O于C,∴∠GCA=∠ABC.
∴∠BAC=∠CAG. 5分
(2)連結(jié)CF,∵EC切⊙O于C, ∴∠ACE=∠AFC.
又∠BAC=∠CAG, ∴△ACF∽△AEC.
∴ ,∴AC2=AE·AF. 10分
,∴AC2=AE·AF. 10分
考點(diǎn):本題主要考查弦切角定理,圓的性質(zhì),三角形相似。
點(diǎn)評(píng):簡單題,利用弦切角定理及三角形相似知識(shí),證明角相等、確定線段長度的關(guān)系,是常見題目。



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,已知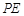 切⊙
切⊙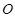 于點(diǎn)E,割線PBA交⊙
于點(diǎn)E,割線PBA交⊙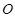 于A、B兩點(diǎn),∠APE的平分線和AE、BE分別交于點(diǎn)C、D.
于A、B兩點(diǎn),∠APE的平分線和AE、BE分別交于點(diǎn)C、D.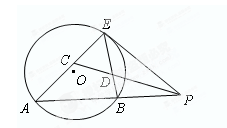
求證:(Ⅰ)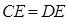 ; (Ⅱ)
; (Ⅱ)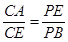 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
在直角坐標(biāo)系中,以坐標(biāo)原點(diǎn)O為極點(diǎn),x軸的正半軸為極軸建立極坐標(biāo)系.已知點(diǎn)A的極坐標(biāo)為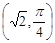 ,直線
,直線 的極坐標(biāo)方程為
的極坐標(biāo)方程為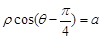 ,且點(diǎn)A在直線
,且點(diǎn)A在直線 上。
上。
(Ⅰ)求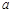 的值及直線
的值及直線 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(Ⅱ)圓C的參數(shù)方程為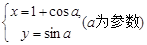 ,試判斷直線l與圓C的位置關(guān)系.
,試判斷直線l與圓C的位置關(guān)系.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
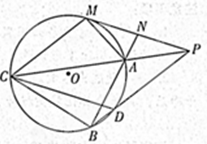
如圖,已知圓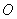 外有一點(diǎn)
外有一點(diǎn)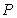 ,作圓
,作圓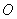 的切線
的切線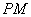 ,
,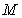 為切點(diǎn),過
為切點(diǎn),過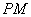 的中點(diǎn)
的中點(diǎn)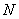 ,作割線
,作割線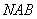 ,交圓于
,交圓于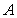 、
、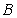 兩點(diǎn),連接
兩點(diǎn),連接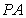 并延長,交圓
并延長,交圓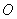 于點(diǎn)
于點(diǎn)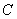 ,連續(xù)
,連續(xù)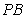 交圓
交圓 于點(diǎn)
于點(diǎn) ,若
,若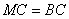 .
.
(1)求證:△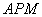 ∽△
∽△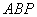 ;
;
(2)求證:四邊形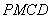 是平行四邊形.
是平行四邊形.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖所示,PA為圓 的切線,A為切點(diǎn),PBC是過點(diǎn)O的割線,PA=10,PB=5,
的切線,A為切點(diǎn),PBC是過點(diǎn)O的割線,PA=10,PB=5,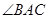 的平分線與BC和圓
的平分線與BC和圓 分別交于點(diǎn)D和E。
分別交于點(diǎn)D和E。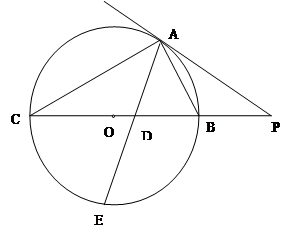
(1)求證: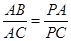 ;
;
(2)求AD·AE的值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,A,B,C,D四點(diǎn)在同一圓上,AD的延長線與BC的延長線交于E點(diǎn),且EC=ED.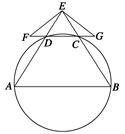
(1)證明:CD∥AB;
(2)延長CD到F,延長DC到G,使得EF=EG,證明:A,B,G,F(xiàn)四點(diǎn)共圓.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分10分)
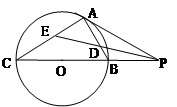
如圖,已知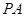 與圓
與圓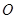 相切于點(diǎn)
相切于點(diǎn)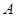 ,經(jīng)過點(diǎn)
,經(jīng)過點(diǎn)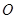 的割線
的割線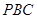 交圓
交圓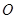 于點(diǎn)
于點(diǎn) 、
、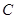 ,
,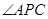 的平分線分別交
的平分線分別交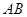 、
、 于點(diǎn)
于點(diǎn) 、
、 .
.
求證:(1) 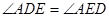 .
.
(2) 若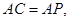 求
求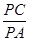 的值.
的值.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com