
已知函數(shù)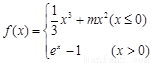
(1)討論函數(shù)f (x)的極值情況;
(2)設(shè)g (x) = ln(x + 1),當(dāng)x1>x2>0時,試比較f (x1 – x2)與g (x1 – x2)及g (x1) –g (x2)三者的大小;并說明理由.
(1)f (x)在(0, +∞)上遞增,故f (x)有極小值f (0)
= 0,f (x)有極大值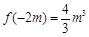 (2)見解析
(2)見解析
【解析】本試題主要考查了分段函數(shù)的極值的問題的運(yùn)用。利用三次函數(shù)的極值的判定結(jié)合證明。以及利用單調(diào)性證明不等式的問題的綜合運(yùn)用。
(1)分別對于兩段函數(shù)的單調(diào)性進(jìn)行判定,確定極值問題。
(2)先對當(dāng)x >0時,先比較ex – 1與ln(x + 1)的大小,
然后得到就是f (x) > g (x) ,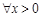 成立.再比較
成立.再比較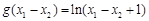 與g (x1) –g (x2) =ln(x1 + 1) –ln(x2
+ 1)的大小.,利用作差法得到證明。
與g (x1) –g (x2) =ln(x1 + 1) –ln(x2
+ 1)的大小.,利用作差法得到證明。
解:(1)當(dāng)x>0時,f (x) = ex – 1在(0,+∞)單調(diào)遞增,且f (x)>0;
當(dāng)x≤0時,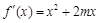 .
.
①若m = 0,f ′(x) = x2≥0, f (x) =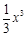 在(–∞,0]上單調(diào)遞增,且f (x) =
在(–∞,0]上單調(diào)遞增,且f (x) =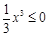 .
.
又f (0) = 0,∴f (x)在R上是增函數(shù),無極植;
②若m<0,f ′(x) = x(x
+ 2m) >0,則f (x) =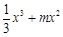 在(–∞,0)單調(diào)遞增,同①可知f (x)在R上也是增函數(shù),無極值; ………………4分
在(–∞,0)單調(diào)遞增,同①可知f (x)在R上也是增函數(shù),無極值; ………………4分
③若m>0,f (x)在(–∞,–2m]上單調(diào)遞增,在(–2m,0)單調(diào)遞減,
又f (x)在(0, +∞)上遞增,故f (x)有極小值f (0) = 0,f
(x)有極大值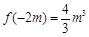 . 6分
. 6分
(2)當(dāng)x >0時,先比較ex – 1與ln(x + 1)的大小,
設(shè)h(x) = ex – 1–ln(x + 1) (x >0)
h′(x) =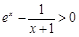 恒成立
恒成立
∴h(x)在(0,+∞)是增函數(shù),h(x)>h (0) = 0
∴ex – 1–ln(x + 1) >0即ex – 1>ln(x + 1)
也就是f (x) > g (x) ,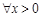 成立.
成立.
故當(dāng)x1 – x2>0時,f (x1 – x2)> g (x1 – x2)……………………………10分
再比較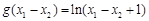 與g (x1) –g (x2) =ln(x1 + 1) –ln(x2
+ 1)的大小.
與g (x1) –g (x2) =ln(x1 + 1) –ln(x2
+ 1)的大小.
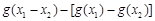 =
=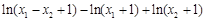
=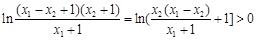
∴g (x1 – x2) > g (x1) –g (x2)
∴f (x1 – x2)> g (x1 – x2) > g (x1) –g (x2) .


 高中必刷題系列答案
高中必刷題系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:2014屆江蘇省揚(yáng)州市高二下學(xué)期期末考試文科數(shù)學(xué)試卷(解析版) 題型:解答題
已知函數(shù)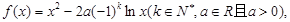
(1)討論函數(shù)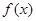 的單調(diào)性;
的單調(diào)性;
(2)若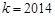 時,關(guān)于
時,關(guān)于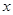 的方程
的方程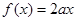 有唯一解,求
有唯一解,求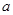 的值;
的值;
(3)當(dāng)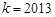 時,證明: 對一切
時,證明: 對一切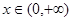 ,都有
,都有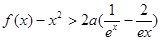 成立.
成立.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年浙江省高三10月月考理科數(shù)學(xué)試卷(解析版) 題型:解答題
已知函數(shù)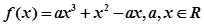
(1)討論函數(shù)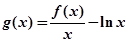 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)如果存在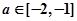 ,使函數(shù)
,使函數(shù)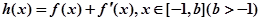 在
在 處取得最小值,試求
處取得最小值,試求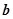 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012屆云南省高三上期中理科數(shù)學(xué)試卷(解析版) 題型:解答題
(本小題滿分12分)已知函數(shù)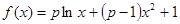 .
.
(1)討論函數(shù)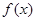 的單調(diào)性;
的單調(diào)性;
(2)當(dāng)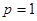 時,
時,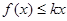 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)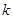 的取值范圍;
的取值范圍;
(3)證明: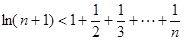
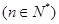 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年湖南省岳陽市高三第三次月考理科數(shù)學(xué) 題型:解答題
已知函數(shù)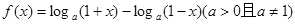
(1)討論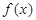 的奇偶性與單調(diào)性;
的奇偶性與單調(diào)性;
(2)若不等式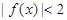 的解集為
的解集為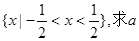 的值;
的值;
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com