已知函數f(x)=ax-lnx+1(a∈R),g(x)=xe1-x.
(1)求函數g(x)在區間(0,e]上的值域T;
(2)是否存在實數a,對任意給定的集合T中的元素t,在區間[1,e]上總存在兩個不同的xi(i=1,2),使得f(xi)=t成立、若存在,求出a的取值范圍;若不存在,請說明理由;
(3 )函數f(x)圖象上是否存在兩點A(x1,y1)和B(x2,y2),使得割線AB的斜率恰好等于函數f(x)在AB中點M(x0,y0)處切線的斜率?請寫出判斷過程.
解:(1)∵g′(x)=e
1-x-xe
1-x=e
1-x(1-x),
∴g(x)在區間(0,1]上單調遞增,在區間[1,e)上單調遞減,
且g(0)=0,g(1)=1>g(e)=e
2-e,
∴g(x)的值域T為(0,1].
(2)則由(1)可得t∈(0,1],
原問題等價于:對任意的t∈(0,1],f(x)=t在[1,e]上總有兩個不同的實根,
故f(x)在[1,e]不可能是單調函數,
∵
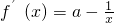
,(1≤x≤e),
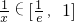
,
當a≥1時,f′(x)>0,f(x)在區間[1,e]上單調遞增,不合題意.
當a

時,f′(x)<0,f(x)在區間[1,e]上單調遞減,不合題意.
當1<
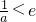
,即

時,f(x)在區間[1,

]上單調遞減;f(x)在區間[
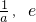
]上單遞增,
由上可得a∈(
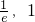
),此時必有f(x)的最小值小于等于0,
且f(x)的最大值大于等于1,
而由f(x)
min=f(

)=2+lna≤0,
可得a
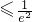
,則a∈∅.
綜上,滿足條件的a不存在.
(3)k
AB=

=
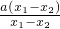
=
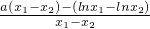
=a-
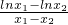
,
而
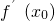
=

=a-

,
故有
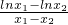
=

,
即
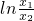
=

=
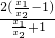
,
令t=
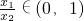
,
則上式化為
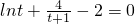
,
令F(t)=lnt+

-2,
則由
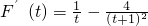
=
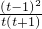
>0,
可得F(t)在(0,1)上單調遞增,
故F(t)<F(1)=0,即方程lnt+
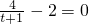
無解,
所以函數f(x)圖象上是不存在兩點A(x
1,y
1)和B(x
2,y
2),
使得割線AB的斜率恰好等于函數f(x)在AB中點M(x
0,y
0)處切線的斜率.
分析:(1)由g′(x)=e
1-x-xe
1-x=e
1-x(1-x),知g(x)在區間(0,1]上單調遞增,在區間[1,e)上單調遞減,由此能求出g(x)的值域T.
(2)則由(1)可得t∈(0,1],原問題等價于:對任意的t∈(0,1],f(x)=t在[1,e]上總有兩個不同的實根,
故f(x)在[1,e]不可能是單調函數,由此能推導出滿足條件的a不存在.
(3)k
AB=

=
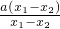
=a-
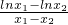
,而
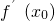
=

=a-

,
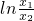
=

=
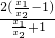
,由此能推導出函數f(x)圖象上是不存在兩點A(x
1,y
1)和B(x
2,y
2),使得割線AB的斜率恰好等于函數f(x)在AB中點M(x
0,y
0)處切線的斜率.
點評:本題考查函數的值域的求法,探索是否存在滿足條件的實數,探索函數圖象上滿足條件的兩點是否存在.綜合性強,難度大,對數學思維能力要求較高,有一定的探索性.

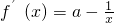 ,(1≤x≤e),
,(1≤x≤e),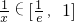 ,
, 時,f′(x)<0,f(x)在區間[1,e]上單調遞減,不合題意.
時,f′(x)<0,f(x)在區間[1,e]上單調遞減,不合題意.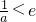 ,即
,即 時,f(x)在區間[1,
時,f(x)在區間[1, ]上單調遞減;f(x)在區間[
]上單調遞減;f(x)在區間[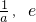 ]上單遞增,
]上單遞增,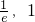 ),此時必有f(x)的最小值小于等于0,
),此時必有f(x)的最小值小于等于0, )=2+lna≤0,
)=2+lna≤0,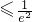 ,則a∈∅.
,則a∈∅. =
=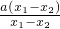
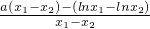
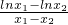 ,
,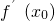 =
= =a-
=a- ,
,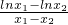 =
= ,
,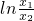 =
= =
=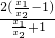 ,
,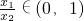 ,
,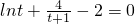 ,
, -2,
-2,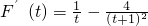 =
=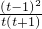 >0,
>0,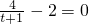 無解,
無解, =
=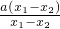 =a-
=a-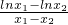 ,而
,而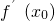 =
= =a-
=a- ,
,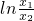 =
= =
=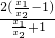 ,由此能推導出函數f(x)圖象上是不存在兩點A(x1,y1)和B(x2,y2),使得割線AB的斜率恰好等于函數f(x)在AB中點M(x0,y0)處切線的斜率.
,由此能推導出函數f(x)圖象上是不存在兩點A(x1,y1)和B(x2,y2),使得割線AB的斜率恰好等于函數f(x)在AB中點M(x0,y0)處切線的斜率.
