
(1)![]()
(2) ![]()
(3)求(1-![]() i)10的展開式中的所有奇數(shù)項(xiàng)的和.
i)10的展開式中的所有奇數(shù)項(xiàng)的和.
分析:對于以上三例若按復(fù)數(shù)乘除法和乘方法直接計(jì)算,則顯得十分繁鎖.若能結(jié)合題目特點(diǎn),聯(lián)想結(jié)論(1±i)2=±2i和ω的性質(zhì),對于(2)題并注意到-2![]() +i=i(1+2
+i=i(1+2![]() i),對于(3)利用二項(xiàng)式定理展開,不難找出簡捷解法.
i),對于(3)利用二項(xiàng)式定理展開,不難找出簡捷解法.
解:(1)原式=
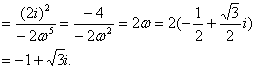
其中ω=-![]() +
+![]() i.
i.
(2)原式=![]()
=i+(![]() )1 003
)1 003
=i+i1 003=i+i4×250+3=i+i3=i-i=0.
(3)∵(1-![]() i)10=1-
i)10=1-![]() ·
·![]() i+
i+![]() ·(
·(![]() i)2-
i)2-![]() ·(
·(![]() i)3+…,
i)3+…,
∴(1-![]() i)10的展開式中奇數(shù)項(xiàng)之和為復(fù)數(shù)(1-3i)10的實(shí)部.
i)10的展開式中奇數(shù)項(xiàng)之和為復(fù)數(shù)(1-3i)10的實(shí)部.
又(1-![]() i)10=[-2·(-
i)10=[-2·(-![]() +
+![]() i)]10=210ω10=210ω=210(-
i)]10=210ω10=210ω=210(-![]() +
+![]() i)=-29+29
i)=-29+29![]() i.
i.
∴(1-![]() i)10的展開式中各奇數(shù)項(xiàng)的和為-29.
i)10的展開式中各奇數(shù)項(xiàng)的和為-29.
點(diǎn)評 代數(shù)形式的復(fù)數(shù)運(yùn)算,基本思路是應(yīng)用法則,但如果能通過對表達(dá)式的結(jié)構(gòu)特征進(jìn)行分析,靈活運(yùn)用i的冪的性質(zhì)、1的立方虛根ω的性質(zhì)以及1±i的冪的性質(zhì)等,將可有效地簡化運(yùn)算,提高效率.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| 3 | (-4)3 |
| 1 |
| 2 |
| 1 |
| 2 |
| -1 | ||
|
| 2lg2+lg3 | ||||
1+
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| 5 |
| 8 |
| 1 |
| 2 |
| 32 |
| 9 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| 1 |
| 4 |
| 7 |
| 8 |
| 3 |
| 8 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| (1-log63)2+log62•log618 |
| log64 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| sin(α+3π)+cos(π+α) | sin(-α)-cos(π+α) |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com