【題目】某中學的甲、乙、丙三名同學參加高校自主招生考試，每位同學彼此獨立的從
四所高校中選2所.
（1）求甲、乙、丙三名同學都選
高校的概率；
（2）若甲必選
，記
為甲、乙、丙三名同學中選校的人數，求隨機變量的分布列及數學期望.
53隨堂測系列答案科目：高中數學 來源： 題型：
【題目】學校藝術節對同一類的
，
，
，
四項參賽作品，只評一項一等獎，在評獎揭曉前，甲、乙、丙、丁四位同學對這四項參賽作品預測如下：
甲說：“是或作品獲得一等獎”；
乙說：“作品獲得一等獎”；
丙說：“，兩項作品未獲得一等獎”；
丁說：“是作品獲得一等獎”.
若這四位同學中只有兩位說的話是對的，則獲得一等獎的作品是__________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，不等式
對
恒成立．
（1）求函數
的極值和函數的圖象在點
處的切線方程；
（2）求實數
的取值的集合
；
（3）設
，函數
，
，其中
為自然對數的底數，若關于
的不等式
至少有一個解
，求
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系xOy中，直線
的參數方程為
（t為參數），以坐標原點為極點，x軸的正半軸為極軸建立極坐標系，已知曲線
的極坐標方程為
，直線與曲線C交于
兩點．
（1）求直線的普通方程和曲線C的直角坐標方程；
（2）求
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某企業有兩個分廠生產某種零件，按規定內徑尺寸（單位：mm）的值落在[29.94，30.06）的零件為優質品.從兩個分廠生產的零件中各抽出了500件，量其內徑尺寸，得結果如下表：
甲廠：
分組 | [29.86，29.90） | [29.90，29.94） | [29.94，29.98） | [29.98，30.02） | [30.02，30.06） | [30.06，30.10） | [30.10，30.14） |
頻數 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
乙廠：
分組 | [29.86，29.90） | [29.90，29.94） | [29.94，29.98） | [29.98，30.02） | [30.02，30.06） | [30.06，30.10） | [30.10，30.14） |
頻數 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
（1）試分別估計兩個分廠生產的零件的優質品率；
（2）由以上統計數據填下面
列聯表，并問是否有
的把握認為“兩個分廠生產的零件的質量有差異”.
甲 廠 | 乙 廠 | 合計 | |
優質品 | |||
非優質品 | |||
合計 |
附： 
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知多面體ABCA1B1C1，A1A，B1B，C1C均垂直于平面ABC，∠ABC=120°，A1A=4，C1C=1，AB=BC=B1B=2．
（Ⅰ）證明：AB1⊥平面A1B1C1；
（Ⅱ）求直線AC1與平面ABB1所成的角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】光伏發電是利用太陽能電池及相關設備將太陽光能直接轉化為電能，近幾年在國內出臺的光伏發電補貼政策的引導下，某地光伏發電裝機量急劇上漲，如下表：
年份 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
年份代碼 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
新增光伏裝機量 | 0.4 | 0.8 | 1.6 | 3.1 | 6.1 | 7.1 | 9.7 | 12.2 |
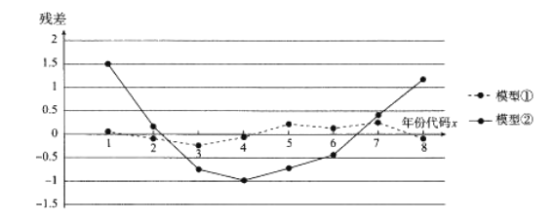
某位同學分別用兩種模型：①
，②
進行擬合，得到相應的回歸方程并進行殘差分析，殘差圖如下（注：殘差等于
）
經過計算得
，
，
，
，其中
，
.
（1）根據殘差圖，比較模型①，②的擬合效果，應該選擇哪個模型？并簡要說明理由.
（2）根據（1）的判斷結果及表中數據建立
關于
的回歸方程，并預測該地區2020年新增光伏裝機量是多少.（在計算回歸系數時精確到0.01）
附：歸直線的斜率和截距的最小二乘估計公式分別為：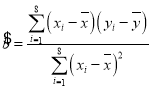
，
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
