
A.6種 B.9種
C.11種 D.23種
分析:將同室4人分別記為甲、乙、丙、丁(或將四張賀卡分別記為A、B、C、D),然后利用四個人取卡的情況分步來確定.
解法一:不妨讓甲、乙、丙、丁四人寫的卡片分別標上號碼為1、2、3、4.顯然完成這件事情需要四步完成:第一步不妨讓甲先拿,有3種方法;第二步讓甲拿的編號的人去拿,有3種方法;第三步、第四步讓剩下兩人去拿,各有1種方法.
∴共有3×3×1×1=9種,應選B.
解法二:設四張賀卡分別記為A、B、C、D.由題意,某人(不妨設A卡的供卡人)取卡的情況有3種,據此將卡的不同分配方式分為三類,對于每一類,其他人依次取卡分步進行,為了避免重復或遺漏現象,我們用“樹圖”表示如下:
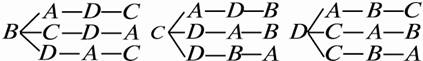
∴共有9種不同的分配方式.
故應選B.
答案:B
點評:本例提供的第一種解法用了分步計數原理.第二種解法可以看作兩個原理的交替應用,用“樹圖”表示一目了然.


科目:高中數學 來源:不詳 題型:單選題
| A.6種 | B.9種 | C.11種 | D.23種 |
查看答案和解析>>
科目:高中數學 來源:2004-2005學年北京市順義十中高一(下)期中后檢測數學試卷2(排列組合部分)(解析版) 題型:選擇題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com