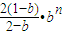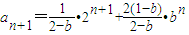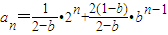設數列{an}的前n項和為Sn,已知ban-2n=(b-1)Sn
(Ⅰ)證明:當b=2時,{an-n•2n-1}是等比數列;
(Ⅱ)求{an}的通項公式.
【答案】
分析:(Ⅰ)當b=2時,由題設條件知a
n+1=2a
n+2
n.由此可知a
n+1-(n+1)•2
n=2a
n+2
n-(n+1)•2
n=2(a
n-n•2
n-1),所以{a
n-n•2
n-1}是首項為1,公比為2的等比數列.
(Ⅱ)當b=2時,由題設條件知a
n=(n+1)2
n-1;當b≠2時,由題意得
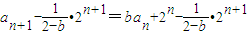
=
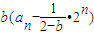
,由此能夠導出{a
n}的通項公式.
解答:解:由題意知a
1=2,且ba
n-2
n=(b-1)S
nba
n+1-2
n+1=(b-1)S
n+1兩式相減得b(a
n+1-a
n)-2
n=(b-1)a
n+1即a
n+1=ba
n+2
n①
(Ⅰ)當b=2時,由①知a
n+1=2a
n+2
n于是a
n+1-(n+1)•2
n=2a
n+2
n-(n+1)•2
n=2(a
n-n•2
n-1)
又a
1-1•2
=1≠0,所以{a
n-n•2
n-1}是首項為1,公比為2的等比數列.
(Ⅱ)當b=2時,由(Ⅰ)知a
n-n•2
n-1=2
n-1,即a
n=(n+1)2
n-1當b≠2時,由①得
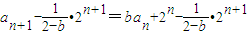
=
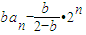
=
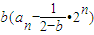
因此
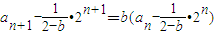
=
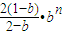
即
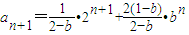
所以
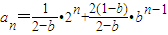 點評:
點評:此題重點考查數列的遞推公式,利用遞推公式求數列的通項公式,同時考查分類討論思想;推移腳標兩式相減是解決含有S
n的遞推公式的重要手段,使其轉化為不含S
n的遞推公式,從而針對性的解決;在由遞推公式求通項公式是重視首項是否可以吸收是易錯點,同時重視分類討論,做到條理清晰是關鍵.

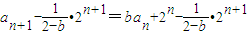 =
=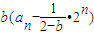 ,由此能夠導出{an}的通項公式.
,由此能夠導出{an}的通項公式.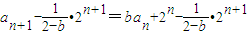 =
=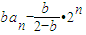 =
=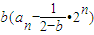
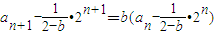 =
=