
設z是虛數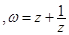 是實數,且
是實數,且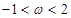 .
.
(1)求|z|的值及z的實部的取值范圍;
(2)設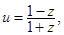 求證:u為純虛數;
求證:u為純虛數;
(3)求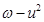 的最小值.
的最小值.
解:(1)∵z是虛數,∴可設z=x+yi R,且
R,且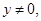 、
、
∴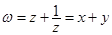 i
i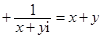 i
i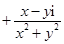
 i.
i.
∵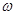 是實數且
是實數且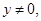 ∴
∴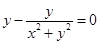 .
.
∴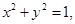 即|z|=1.此時
即|z|=1.此時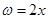 .
.
∵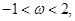 ∴-1<2x<2,從而有
∴-1<2x<2,從而有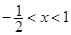 .
.
即z的實部的取值范圍是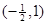 .
.
(2)證法一: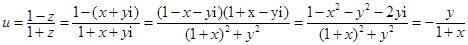 i,
i,
∵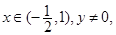 ∴
∴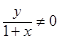 .∴u為純虛數.
.∴u為純虛數.
證法二:∵z為虛數,且|z|=1 ,∴z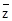 =1
, 即
=1
, 即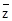
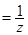 .
.
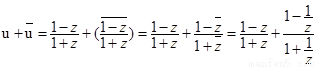
 .
.
∴u為純虛數.
(3)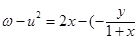 i
i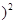 ?
?
 2x+
2x+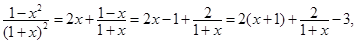
∵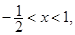 ∴1+x>0.
∴1+x>0.
于是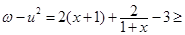
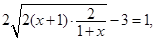
當且僅當2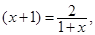 即x=0時等號成立.
即x=0時等號成立.
∴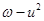 的最小值為1,此時
的最小值為1,此時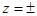 i.
i.
【解析】本試題主要是考查了復數的概念和運算的綜合運用
(1)因為z是虛數,∴可設z=x+yi R,且
R,且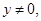 、
、
∴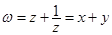 i
i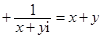 i
i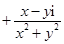
從而證明u是純虛數。
(2)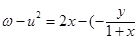 i
i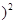 ,然后化簡和計算得到
,然后化簡和計算得到
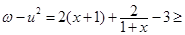
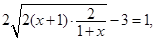 然后借助于函數思想得到結論。
然后借助于函數思想得到結論。


 閱讀快車系列答案
閱讀快車系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com