
 中,若
中,若 ,則
,則 ;
; 的三個內角,則
的三個內角,則 的最小值為
的最小值為

 ,則數列
,則數列 中的最小項為
中的最小項為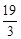 ;
; ,且
,且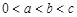 ,則
,則 ;
; 的最小值為
的最小值為 .
. 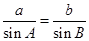
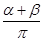 =1,
=1,
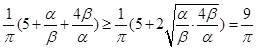 ,
, ,即α=2β時取等號.所以②正確.
,即α=2β時取等號.所以②正確. =2+
=2+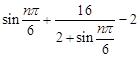 ,因為1≤
,因為1≤ ≤3,
≤3, ,則1≤t≤3.因為函數y=t+
,則1≤t≤3.因為函數y=t+ -2在區間(0,4)上單調遞減,所以在[1,3]上單調遞減,因此,當t=3時,函數有最小值3+
-2在區間(0,4)上單調遞減,所以在[1,3]上單調遞減,因此,當t=3時,函數有最小值3+ -2=
-2= ,則對應數列{an}中的最小項為
,則對應數列{an}中的最小項為 ,所以③正確.
,所以③正確.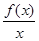 ,則函數g(x)的幾何意義為曲線上點與原點連線斜率的大小.由題意可知
,則函數g(x)的幾何意義為曲線上點與原點連線斜率的大小.由題意可知 ,
, 分別看作函數f(x)=log2(x+1)圖象上的點(a,f(a)),(b,f(b)),(c,f(b))與原點連線的斜率,由圖象可知,
分別看作函數f(x)=log2(x+1)圖象上的點(a,f(a)),(b,f(b)),(c,f(b))與原點連線的斜率,由圖象可知,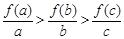 ,所以④錯誤.
,所以④錯誤.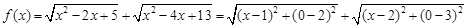 ,問題轉化成點P(x,0)到A(1,2),B(2,3)距離之和的最小值。原式等價為|PA|+|PB|的最小值,找出點A關于x軸的對稱點D(1,-2).
,問題轉化成點P(x,0)到A(1,2),B(2,3)距離之和的最小值。原式等價為|PA|+|PB|的最小值,找出點A關于x軸的對稱點D(1,-2).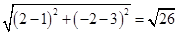 .
.

 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:不詳 題型:解答題
 是時間
是時間 ,單位:
,單位: 的函數,記作:
的函數,記作: ,下表是該港口在某季每天水深的數據:
,下表是該港口在某季每天水深的數據:
 的曲線可以近似地看做函數
的曲線可以近似地看做函數 的圖象.
的圖象. 的近似表達式;
的近似表達式; 以上時認為是安全的(船舶停靠時,船底只需不碰到海底即可),某船吃水深度(船底離水面的距離)為
以上時認為是安全的(船舶停靠時,船底只需不碰到海底即可),某船吃水深度(船底離水面的距離)為 ,如果該船想在同一天內安全進出港,問它至多能在港內停留多長時間(忽略進出港所需時間)?
,如果該船想在同一天內安全進出港,問它至多能在港內停留多長時間(忽略進出港所需時間)?查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com