
【題目】有如下命題:①函數y=sinx與y=x的圖象恰有三個交點;②函數y=sinx與y=![]() 的圖象恰有一個交點;③函數y=sinx與y=x2的圖象恰有兩個交點;④函數y=sinx與y=x3的圖象恰有三個交點,其中真命題的個數為( )
的圖象恰有一個交點;③函數y=sinx與y=x2的圖象恰有兩個交點;④函數y=sinx與y=x3的圖象恰有三個交點,其中真命題的個數為( )
A.1B.2C.3D.4
【答案】C
【解析】
①構造函數f(x)=sinx-x,求出函數的導數,研究函數的導數和單調性,進行判斷即可;
②利用![]() 與x的關系進行轉化判斷;
與x的關系進行轉化判斷;
③和④直接作出兩個函數的圖象即可進行判斷.
①設f(x)=sinx-x,則f′(x)=cosx-1≤0,即函數f(x)為減函數,
∵f(0)=0,
∴函數f(x)只有一個零點,即函數y=sinx與y=x的圖象恰有一個交點,故①錯誤,
②由①知當x>0時,sinx<x,
當0<x≤1時,![]() >x>sinx,
>x>sinx,
當x>1時,![]() >sinx,
>sinx,
當x=0時,sinx=![]() ,綜上當x>0時,
,綜上當x>0時,![]() >sinx恒成立,
>sinx恒成立,
函數y=sinx與y=![]() 的圖象恰有一個交點,故②正確,
的圖象恰有一個交點,故②正確,
③作出函數y=sinx與y=x2,的圖象,由圖象知兩個函數有2個交點,即函數y=sinx與y=x2的圖象恰有兩個交點,故③正確,
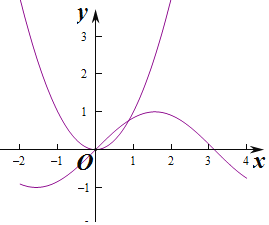
④作出函數y=sinx與y=x3,的圖象,由圖象知兩個函數有3個交點,即函數y=sinx與y=x3的圖象恰有三個交點,故④正確,

故正確的是②③④,
故選C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】中國歷法推測遵循以測為輔、以算為主的原則.例如《周髀算經》和《易經》里對二十四節氣的晷(guǐ)影長的記錄中,冬至和夏至的晷影長是實測得到的,其它節氣的晷影長則是按照等差數列的規律計算得出的.下表為《周髀算經》對二十四節氣晷影長的記錄,其中![]() 寸表示115寸
寸表示115寸![]() 分(1寸=10分).
分(1寸=10分).
節氣 | 冬至 | 小寒 (大雪) | 大寒 (小雪) | 立春 (立冬) | 雨水 (霜降) | 驚蟄 (寒露) | 春分 (秋分) | 清明 (白露) | 谷雨 (處暑) | 立夏 (立秋) | 小滿 (大暑) | 芒種 (小暑) | 夏至 |
晷影長 (寸 | 135 |
|
|
|
|
| 75.5 |
|
|
|
|
| 16.0 |
已知《易經》中記錄某年的冬至晷影長為130.0寸,夏至晷影長為14.8寸,按照上述規律那么《易經》中所記錄的春分的晷影長應為( )
A.91.6寸B.82.0寸C.81.4寸D.72.4寸
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,曲線C1的參數方程為![]() (θ為參數),以原點為極點,x軸非負半軸為極軸,建立極坐標系,曲線C2的極坐標方程為
(θ為參數),以原點為極點,x軸非負半軸為極軸,建立極坐標系,曲線C2的極坐標方程為![]() .
.
(1)求曲線C1的極坐標方程以及曲線C2的直角坐標方程;
(2)若直線l:y=kx與曲線C1、曲線C2在第一象限交于P、Q,且|OQ|=|PQ|,點M的直角坐標為(1,0),求△PMQ的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() -x2+ef′(
-x2+ef′(![]() )x.
)x.
(Ⅰ)求f(x)的單調區間;
(Ⅱ)若存在x1,x2(x1<x2),使得f(x1)+f(x2)=1,求證:x1+x2<2.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐![]() 中,
中,![]() 平面
平面![]() ,
,![]() 是正三角形,
是正三角形,![]() 與
與![]() 的交點
的交點![]() 恰好是
恰好是![]() 中點,又
中點,又![]() ,
,![]() .
.

(1)求證:![]() ;
;
(2)設![]() 為
為![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上,若直線
上,若直線![]() 平面
平面![]() ,求
,求![]() 的長;
的長;
(3)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,定義![]() 為兩點
為兩點![]() ,
,![]() 的“切比雪夫距離”,又設點
的“切比雪夫距離”,又設點![]() 及
及![]() 上任意一點
上任意一點![]() ,稱
,稱![]() 的最小值為點
的最小值為點![]() 到直線
到直線![]() 的“切比雪夫距離”,記作
的“切比雪夫距離”,記作![]() ,給出下列三個命題:
,給出下列三個命題:
①對任意三點![]() 、
、![]() 、
、![]() ,都有
,都有![]() ;
;
②已知點![]() 和直線
和直線![]() :
:![]() ,則
,則![]() ;
;
③到定點![]() 的距離和到
的距離和到![]() 的“切比雪夫距離”相等的點的軌跡是正方形.
的“切比雪夫距離”相等的點的軌跡是正方形.
其中正確的命題有( )
A.0個B.1個C.2個D.3個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查各校學生體質健康達標情況,某機構M采用分層抽樣的方法從![]() 校抽取了
校抽取了![]() 名學生進行體育測試,成績按照以下區間分為七組:[30,40),[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],并得到如下頻率分布直方圖.根據規定,測試成績低于60分為體質不達標.已知本次測試中不達標學生共有20人.
名學生進行體育測試,成績按照以下區間分為七組:[30,40),[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],并得到如下頻率分布直方圖.根據規定,測試成績低于60分為體質不達標.已知本次測試中不達標學生共有20人.
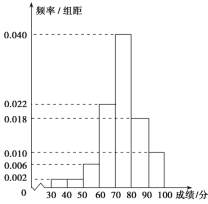
(1)求![]() 的值;
的值;
(2)現從![]() 校全體同學中隨機抽取2人,以頻率作為概率,記
校全體同學中隨機抽取2人,以頻率作為概率,記![]() 表示成績不低于90分的人數,求
表示成績不低于90分的人數,求![]() 的分布列及數學期望;
的分布列及數學期望;
(3)另一機構N也對該校學生做同樣的體質達標測試,并用簡單隨機抽樣方法抽取了100名學生,經測試有20名學生成績低于60分.計算兩家機構測試成績的不達標率,你認為用哪一個值作為對該校學生體質不達標率的估計較為合理,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com