
【題目】隨著智能手機的發展,微信越來越成為人們交流的一種方式,某機構對使用微信交流的態度進行調查,隨機調查了50人,他們年齡的頻數分布及對使用微信交流贊成人數如表:
年齡(歲) |
|
|
|
|
|
|
頻數 | 5 | 10 | 15 | 10 | 5 | 5 |
贊成人數 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)由以上統計數據填寫下面![]() 列聯表,并判斷是否有99%的把握認為年齡45歲為分界點對使用微信交流的態度有差異;
列聯表,并判斷是否有99%的把握認為年齡45歲為分界點對使用微信交流的態度有差異;
年齡不低于45歲的人 | 年齡低于45歲的人 | 合計 | |
贊成 | |||
不贊成 | |||
合計 |
(2)若對年齡分別在![]() ,
, ![]() 的被調查人中各抽取一人進行追蹤調查,求選中的2人中至少有一人贊成使用微信交流的概率.
的被調查人中各抽取一人進行追蹤調查,求選中的2人中至少有一人贊成使用微信交流的概率.
參考公式: ![]() ,其中
,其中![]()
參考數據:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【答案】(I)見解析;(Ⅱ)見解析
【解析】試題分析:(I)由題意,完成 2×2 列聯表,利用獨立性檢驗的公式,求解![]() 的值,對比,即可得出結論;
的值,對比,即可得出結論;
(Ⅱ)根據題意,確定隨機變量![]() 的所有可能取值,根據相互獨立事件的概率公式求解相應的概率,列出分布列,代入期望的公式,即可求解數學期望.
的所有可能取值,根據相互獨立事件的概率公式求解相應的概率,列出分布列,代入期望的公式,即可求解數學期望.
試題解析:
(I)由以上統計數據填寫下面 2×2 列聯表,如下;
年齡不低于45歲的人 | 年齡低于45歲的人 | 合計 | |
贊成 | 10 | 27 | 37 |
不贊成 | 10 | 3 | 13 |
合計 | 20 | 30 | 50 |
根據公式計算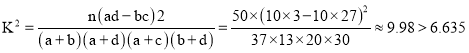 ,
,
所以有99%的把握認為年齡45歲為分界點對使用微信交流的態度有差異;
(Ⅱ)根據題意,X的所有可能取值為0,1,2,3,
則![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
隨機變量X的分布列為:
| 0 | 1 | 2 | 3 |
P |
|
|
|
|
所以X的數學期望為![]()


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:高中數學 來源: 題型:
【題目】已知 (
(![]() ,
, ![]() )展開式的前三項的二項式系數之和為16,所有項的系數之和為1.
)展開式的前三項的二項式系數之和為16,所有項的系數之和為1.
(1)求![]() 和
和![]() 的值;
的值;
(2)展開式中是否存在常數項?若有,求出常數項;若沒有,請說明理由;
(3)求展開式中二項式系數最大的項.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]() (θ為參數),將
(θ為參數),將![]() 上的所有點的橫坐標、縱坐標分別伸長為原來的
上的所有點的橫坐標、縱坐標分別伸長為原來的![]() 和2倍后得到曲線
和2倍后得到曲線![]() ,以平面直角坐標系
,以平面直角坐標系![]() 的原點
的原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸,取相同的單位長度建立極坐標系,已知直線
軸的正半軸為極軸,取相同的單位長度建立極坐標系,已知直線![]() .
.
(1)試寫出曲線![]() 的極坐標方程與曲線
的極坐標方程與曲線![]() 的參數方程;
的參數方程;
(2)在曲線![]() 上求一點
上求一點![]() ,使點
,使點![]() 到直線
到直線![]() 的距離最小,并求此最小值.
的距離最小,并求此最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)已知函數![]() 是自然對數的底數,
是自然對數的底數, ![]() .
.
(1)求函數![]() 的單調遞增區間;
的單調遞增區間;
(2)若![]() 為整數,
為整數, ![]() ,且當
,且當![]() 時,
時, ![]() 恒成立,其中
恒成立,其中![]() 為
為![]() 的導函數,求
的導函數,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查某生產線上質量監督員甲對產品質量好壞有無影響,現統計數據如下:質量監督員甲在生產現場時,990件產品中合格品有982件,次品有8件;甲不在生產現場時,510件產品中合格品有493件,次品有17件,試分別用列聯表、獨立性檢驗的方法分析監督員甲是否在生產現場對產品質量好壞有無影響?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程.
已知曲線![]() 在直角坐標系
在直角坐標系![]() 下的參數方程為
下的參數方程為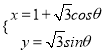 (
(![]() 為參數).以
為參數).以![]() 為極點,
為極點, ![]() 軸的非負半軸為極軸建立極坐標系.
軸的非負半軸為極軸建立極坐標系.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)直線![]() 的極坐標方程是
的極坐標方程是![]() ,射線
,射線![]() 與曲線
與曲線![]() 交于
交于![]() 點,與直線
點,與直線![]() 交于
交于![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的通項公式是
的通項公式是![]() .
.
(1)判斷![]() 是否是數列
是否是數列![]() 中的項;
中的項;
(2)試判斷數列![]() 中的各項是否都在區間
中的各項是否都在區間![]() 內;
內;
(3)試判斷在區間![]() 內是否有無窮數列
內是否有無窮數列![]() 中的項?若有,是第幾項?若沒有,請說明理由.
中的項?若有,是第幾項?若沒有,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com