
【題目】為了讓學生了解環保知識,增強環保意識,某中學舉行了一次環保知識競賽,共有900名學生參加了這次競賽.為了了解本次競賽的成績情況,從中抽取了部分學生的成績(得分取正整數,滿分為100分)進行統計.請你根據下面尚未完成的頻率分布表和頻率分布直方圖(如圖),解答下列問題:
分組 | 頻數 | 頻率 |
[50,60) | 4 | 0.08 |
[60,70) | 8 | 0.16 |
[70,80) | 10 | 0.20 |
[80,90) | 16 | 0.32 |
[90,100] | ||
合計 |
(1)填充頻率分布表中的空格;
(2)不具體計算頻率/組距,補全頻率分布直方圖.

【答案】(1)12,0.24,50,1; (2)見解析.
【解析】
試題分析:(1)由題根據頻率分布表,知各組頻率和為1,可推出[90,100],的頻率并進而得出頻數。再補全頻率分布直方圖。特別注意:縱坐標為頻率除以組距。
(2)由(1)根據頻率分布直方圖算平均值的算法為,取各組的組中值乘以它的頻率,再分別相加可得。
試題解析:(Ⅰ)抽取學生總數=![]()
50-(4+8+10+16)=12,![]()
所以,在區間[90,100]的頻數為12,頻率為0.24;
合計的頻數為50,頻率為1.00.
補全的頻率分布直方圖
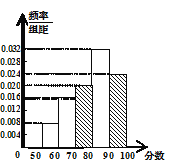
(Ⅱ)平均值為55×0.08+65×0.16+75×0.20+85×0.32+95×0.24=79.8.
所以,學生成績的平均值為79.8.


科目:高中數學 來源: 題型:
【題目】數列{an}中,a1=2, ![]() (n∈N*).
(n∈N*).
(1)證明數列 ![]() 是等比數列,并求數列{an}的通項公式;
是等比數列,并求數列{an}的通項公式;
(2)設 ![]() ,若數列{bn}的前n項和是Tn , 求證:
,若數列{bn}的前n項和是Tn , 求證: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某玩具生產公司每天計劃生產衛兵、騎兵、傘兵這三種玩具共![]() 個,生產一個衛兵需
個,生產一個衛兵需![]() 分鐘,生產一個騎兵需
分鐘,生產一個騎兵需![]() 分鐘,生產一個傘兵需
分鐘,生產一個傘兵需![]() 分鐘,已知總生產時間不超過
分鐘,已知總生產時間不超過![]() 小時,若生產一個衛兵可獲利潤
小時,若生產一個衛兵可獲利潤![]() 元,生產一個騎兵可獲利潤
元,生產一個騎兵可獲利潤![]() 元,生產一個傘兵可獲利潤
元,生產一個傘兵可獲利潤![]() 元.
元.
(1)用每天生產的衛兵個數![]() 與騎兵個數
與騎兵個數![]() 表示每天的利潤
表示每天的利潤![]() (元);
(元);
(2)怎么分配生產任務才能使每天的利潤最大,最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點到準線的距離為
的焦點到準線的距離為![]() ,直線
,直線![]() 與拋物線
與拋物線![]() 交于
交于![]() 兩點,過這兩點分別作拋物線
兩點,過這兩點分別作拋物線![]() 的切線,且這兩條切線相交于點
的切線,且這兩條切線相交于點![]() .
.
(1)若![]() 的坐標為
的坐標為![]() ,求
,求![]() 的值;
的值;
(2)設線段![]() 的中點為
的中點為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,過
,過![]() 的直線
的直線![]() 與線段
與線段![]() 為直徑的圓相切,切點為
為直徑的圓相切,切點為![]() ,且直線
,且直線![]() 與拋物線
與拋物線![]() 交于
交于![]() 兩點,證明:
兩點,證明:  .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 為
為![]() 的中點,
的中點, ![]() 為
為![]() 的中點,
的中點, ![]() 在棱
在棱![]() 上.
上.
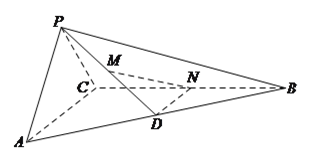
(![]() )當
)當![]() 為
為![]() 的中點時,證明:
的中點時,證明: ![]() 平面
平面![]() .
.
(![]() )求證:
)求證: ![]() 平面
平面![]() .
.
(![]() )是否存在點
)是否存在點![]() 使得
使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,說明理由.
的值,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是矩形,AB=1,BC=![]() ,AA1=2,E是側棱BB1的中點.
,AA1=2,E是側棱BB1的中點.
(1)求證:A1E⊥平面AED;
(2)求二面角A﹣A1D﹣E的大小.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線關于![]() 軸對稱,它的頂點在坐標原點,點
軸對稱,它的頂點在坐標原點,點![]() 在拋物線上.
在拋物線上.
(1)寫出該拋物線的標準方程及其準線方程;
(2)過點![]() 作兩條傾斜角互補的直線與拋物線分別交于不同的兩點
作兩條傾斜角互補的直線與拋物線分別交于不同的兩點![]() ,求證:直線
,求證:直線![]() 的斜率是一個定值.
的斜率是一個定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com