
 km.D為海灣一側海岸線CT上的一點,設CD=x(km),點D對跑道AB的視角為q.
km.D為海灣一側海岸線CT上的一點,設CD=x(km),點D對跑道AB的視角為q.
 ;(2)
;(2)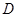 點距
點距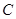 點6km.
點6km. ,因此為了求
,因此為了求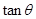 ,可通過求
,可通過求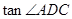 和
和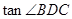 ,
,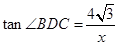 ,下面關鍵要求
,下面關鍵要求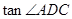 ,為止作
,為止作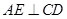 ,垂足為
,垂足為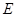 ,這時會發現隨
,這時會發現隨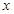 的取值不同,
的取值不同,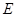 點可能在線段
點可能在線段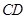 上,也可能在線段
上,也可能在線段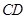 外,
外,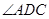 可能為銳角也可能為鈍角,這里出現了分類討論,作
可能為銳角也可能為鈍角,這里出現了分類討論,作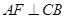 交
交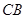 延長線于
延長線于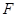 ,由已知可求出
,由已知可求出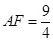 ,這就是分類的分界點;(2)由(1)求得
,這就是分類的分界點;(2)由(1)求得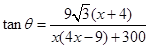 ,要求它的最大值,可以采取兩種方法,一種是由于分子是一次,分母是二次的,可把分子
,要求它的最大值,可以采取兩種方法,一種是由于分子是一次,分母是二次的,可把分子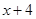 作為整體,分子分母同時除以
作為整體,分子分母同時除以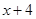 (當然分母也已經化為
(當然分母也已經化為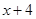 的多項式了),再用基本不等式求解,也可用導數知識求得最大值.
的多項式了),再用基本不等式求解,也可用導數知識求得最大值. ,∠ABF=90o-60o=30o,
,∠ABF=90o-60o=30o,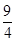 ,BF=4.5×cos30o=
,BF=4.5×cos30o= ,
,
 .
.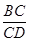 =
=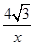 .
.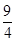 時,ED=x-
時,ED=x-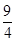 ,tan∠ADC=
,tan∠ADC=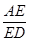 =
=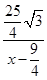 =
=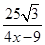 (如圖1);
(如圖1);
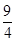 時,ED=
時,ED=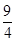 -x,tan∠ADC=-
-x,tan∠ADC=-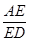 =
=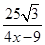 (如圖2). 4分
(如圖2). 4分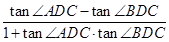
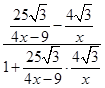 =
=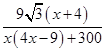 ,其中x>0且x≠
,其中x>0且x≠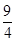 .
. 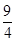 時tanq=
時tanq=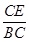 =
=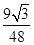 ,符合上式.
,符合上式.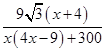 ( x>0) 8分
( x>0) 8分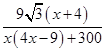 =
= ,x>0. 11分
,x>0. 11分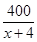 -41≥2
-41≥2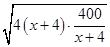 -41=39,
-41=39,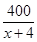 ,即x=6時取等號.
,即x=6時取等號.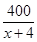 -41取最小值39.
-41取最小值39.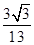 . 13分
. 13分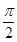 )上是增函數,所以當x=6時,q取最大值.
)上是增函數,所以當x=6時,q取最大值.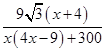 =
=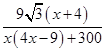 .
.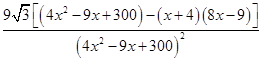 =-
=-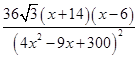 ,x>0.
,x>0.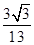 . 13分
. 13分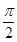 )上是增函數,所以當x=6時,q取最大值.
)上是增函數,所以當x=6時,q取最大值.

科目:高中數學 來源:不詳 題型:解答題
 ,其中,角θ的頂點與坐標原點重合,始邊與x軸非負半軸重合,終邊經過點P(x,y),且0≤θ≤π.
,其中,角θ的頂點與坐標原點重合,始邊與x軸非負半軸重合,終邊經過點P(x,y),且0≤θ≤π. ,求f(θ)的值;
,求f(θ)的值; 上的一個動點,試確定角θ的取值范圍,并求函數f(θ)的最小值和最大值.
上的一個動點,試確定角θ的取值范圍,并求函數f(θ)的最小值和最大值.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題

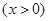 ,其中
,其中 ,
, 為正整數,
為正整數,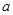 ,
, ,
, 均為常數,曲線
均為常數,曲線 在
在 處的切線方程為
處的切線方程為 .
.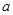 ,
, ,
, 的值;
的值;  的最大值;
的最大值; 都有
都有 .(
.( 為自然對數的底)
為自然對數的底)查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
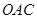 區域內建造甲、乙兩種通信信號加強中轉站,甲中轉站建在區域
區域內建造甲、乙兩種通信信號加強中轉站,甲中轉站建在區域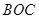 內,乙中轉站建在區域
內,乙中轉站建在區域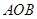 內.分界線
內.分界線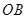 固定,且
固定,且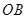 =
=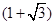 百米,邊界線
百米,邊界線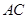 始終過點
始終過點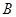 ,邊界線
,邊界線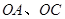 滿足
滿足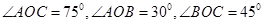 .
.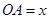 (
(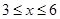 )百米,
)百米,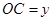 百米.
百米.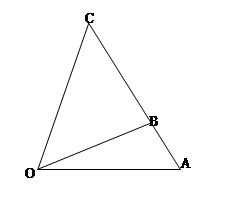
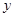 表示成
表示成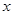 的函數,并求出函數
的函數,并求出函數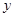 的解析式;
的解析式;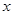 取何值時?整個中轉站的占地面積
取何值時?整個中轉站的占地面積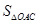 最小,并求出其面積的最小值.
最小,并求出其面積的最小值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com