【答案】
分析:(Ⅰ)解法一:設直線AB的方程為y=k(x-1)+3,代入3x
2+y
2=λ,整理得:(k
2+3)x
2-2k(k-3)x+(k-3)
2-λ=0,然后結合題設條件由根與經數的關系和根的判別式能夠求出直線AB的方程.
解法二:設A(x
1,y
1),B(x
2,y
2),則有
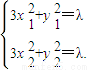
⇒3 (x
1-x
2) (x
1+x
2)+(y
1-y
2)=0.∴k
AB=-
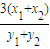
.∵N(1,3)是AB的中點∴k
AB=-1.由此能夠求出直線AB的方程.
(Ⅱ)解法一:由題意知直線CD的方程為x-y+2=0代入橢圓方程,整理得4x
2+4x+4-λ=0.由弦長公式可得|CD|=
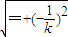
•|x
3-x
4|=

.將直線AB的方程x+y-4=0代入橢圓方程得4x
2-8x+16-λ=0.同理可得|AB|=
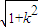
•|x
1-x
2|=

.由此可以推出存在這樣的λ,使得A、B、C、D四點在同一個圓上.
解法二:由題高設條件可知λ>12,直線CD的方程為y-3=x-1,代入橢圓方程,整理得4x
2+4x+4-λ=0.將直線AB的方程x+y-4=0代入橢圓方程整理得4x
2-8x+16-λ=0,由此通過計算知
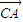
•
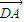
=0,∴A在以CD為直徑的圓上.又B為A關于CD的對稱點,∴A、B、C、D四點共圓.
解答:解:(Ⅰ)解法一:依題意,可設直線AB的方程為y=k(x-1)+3,
代入3x
2+y
2=λ,整理得:(k
2+3)x
2-2k(k-3)x+(k-3)
2-λ=0①
設A(x
1,y
1),B(x
2,y
2),則x
1,x
2是方程①的兩個不同的根,
∴△=4[λ(k
2+3)-3(k-3)
2]>0,②
且x
1+x
2=
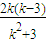
.由N(1,3)是線段AB的中點,得x
1+x
2=2,
∴k(k-3)=k
2+3解得k=-1,代入②得λ>12,
即λ的取值范圍是(12,+∞).
于是直線AB的方程為y-3=-(x-1),即x+y-4=0.
解法二:設A(x
1,y
1),B(x
2,y
2),則有
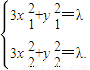
⇒3 (x
1-x
2) (x
1+x
2)+(y
1-y
2)=0.
依題意,x
1≠x
2,∴k
AB=-
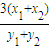
.
∵N(1,3)是AB的中點,∴x
1+x
2=2,y
1+y
2=6,從而k
AB=-1.
又由N(1,3)在橢圓內,∴λ>3×1
2+3
2=12,
∴λ的取值范圍是(12,+∞).
直線AB的方程為y-3=-(x-1),即x+y-4=0.
(Ⅱ)解法一:∵CD垂直平分AB,
∴直線CD的方程為y-3=x-1,即x-y+2=0代入橢圓方程,整理得4x
2+4x+4-λ=0.③
又設C(x
3,y
3),D(x
4,y
4),CD的中點為M(x
,y
),
則x
3,x
4是方程③的兩根,
∴x
3+x
4=-1,且x
=
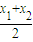
=-

,y
=x
+2=

,即M(
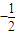
,

)
于是由弦長公式可得|CD|=
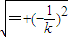
•|x
3-x
4|=
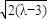
.④
將直線AB的方程x+y-4=0代入橢圓方程得4x
2-8x+16-λ=0.⑤
同理可得|AB|=
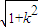
•|x
1-x
2|=

.⑥
∵當λ>12時,
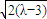
>
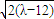
,
∴|AB|<|CD|.
假設存在λ>12,使得A、B、C、D四點共圓,則CD必為圓的直徑,點M為圓心.
點M到直線AB的距離為d=
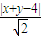
=
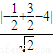
=
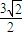
.⑦
于是,由④⑥⑦式及勾股定理可得|MA|
2=|MB|
2=d
2+
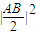
=

+
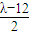
=
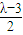
=
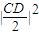
.
故當λ>12時,A、B、C、D四點均在以M為圓心,|
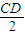
|為半徑的圓上.
(注:上述解法中最后一步可按如下解法獲得:
A、B、C、D共圓?ACD為直角三角形,A為直角?|AN|
2=|CN|•|DN|,
即
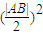
=(|
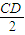
|+d)(|

|-d).⑧
由⑥式知,⑧式左邊=

,
由④⑦知,⑧式右邊=(
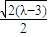
+

)(

-
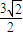
)=
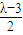
-

=
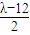
.
∴⑧式成立,即A、B、C、D四點共圓.)
解法二:由(Ⅱ)解法一知λ>12,
∵CD垂直平分AB,
∴直線CD的方程為y-3=x-1,代入橢圓方程,整理得4x
2+4x+4-λ=0.③
將直線AB的方程x+y-4=0代入橢圓方程整理得4x
2-8x+16-λ=0.⑤
解③和⑤式可得x
1,2=
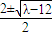
,x
3,4=

,
不妨設A(1+
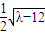
,3-
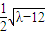
),
C(
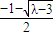
,
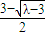
),D(
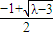
,

).
∴
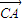
=(

,
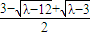
),

=(
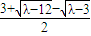
,
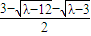
),
計算可得
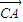
•
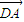
=0,
∴A在以CD為直徑的圓上.
又B為A關于CD的對稱點,
∴A、B、C、D四點共圓.
點評:本題綜合考查直線和橢圓的位置關系,難度較大,解題時要仔細審題,注意公式的靈活運用.

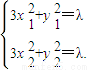 ⇒3 (x1-x2) (x1+x2)+(y1-y2)=0.∴kAB=-
⇒3 (x1-x2) (x1+x2)+(y1-y2)=0.∴kAB=-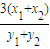 .∵N(1,3)是AB的中點∴kAB=-1.由此能夠求出直線AB的方程.
.∵N(1,3)是AB的中點∴kAB=-1.由此能夠求出直線AB的方程.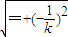 •|x3-x4|=
•|x3-x4|= .將直線AB的方程x+y-4=0代入橢圓方程得4x2-8x+16-λ=0.同理可得|AB|=
.將直線AB的方程x+y-4=0代入橢圓方程得4x2-8x+16-λ=0.同理可得|AB|=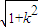 •|x1-x2|=
•|x1-x2|= .由此可以推出存在這樣的λ,使得A、B、C、D四點在同一個圓上.
.由此可以推出存在這樣的λ,使得A、B、C、D四點在同一個圓上.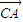 •
•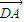 =0,∴A在以CD為直徑的圓上.又B為A關于CD的對稱點,∴A、B、C、D四點共圓.
=0,∴A在以CD為直徑的圓上.又B為A關于CD的對稱點,∴A、B、C、D四點共圓.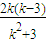 .由N(1,3)是線段AB的中點,得x1+x2=2,
.由N(1,3)是線段AB的中點,得x1+x2=2,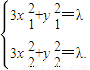 ⇒3 (x1-x2) (x1+x2)+(y1-y2)=0.
⇒3 (x1-x2) (x1+x2)+(y1-y2)=0.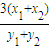 .
.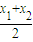 =-
=- ,y=x+2=
,y=x+2= ,即M(
,即M(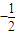 ,
, )
)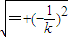 •|x3-x4|=
•|x3-x4|=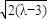 .④
.④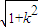 •|x1-x2|=
•|x1-x2|= .⑥
.⑥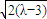 >
>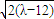 ,
,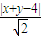 =
=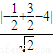 =
=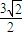 .⑦
.⑦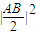 =
= +
+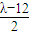 =
=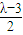 =
=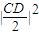 .
.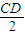 |為半徑的圓上.
|為半徑的圓上.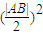 =(|
=(|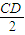 |+d)(|
|+d)(| |-d).⑧
|-d).⑧ ,
,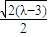 +
+ )(
)( -
-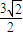 )=
)=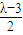 -
- =
=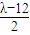 .
.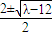 ,x3,4=
,x3,4= ,
,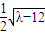 ,3-
,3-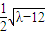 ),
),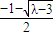 ,
,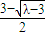 ),D(
),D(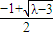 ,
, ).
).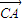 =(
=( ,
,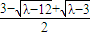 ),
), =(
=(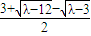 ,
,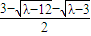 ),
),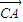 •
•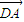 =0,
=0,

 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案 小學教材完全解讀系列答案
小學教材完全解讀系列答案