
 .
.
 ,構造一個關于m的方程,解方程即可得到滿足條件的m的值.
,構造一個關于m的方程,解方程即可得到滿足條件的m的值.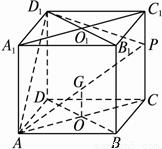 解法一(幾何法):
解法一(幾何法):
 =
=

 PC=
PC= .
. =3
=3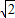
 .?
.? 時,直線AP與平面BDD1B1所成角的正切值為3
時,直線AP與平面BDD1B1所成角的正切值為3 .?
.?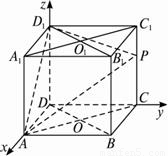
 =(0,0,1)為平面DBC一個法向量,
=(0,0,1)為平面DBC一個法向量,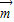 =(x,y,z)為平面C1DB的一個法向量,則
=(x,y,z)為平面C1DB的一個法向量,則 即
即
 =(1,-1,1)
=(1,-1,1) =
=
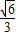 ,tanθ=
,tanθ=

 =(-1,1,0),
=(-1,1,0), =(0,0,1),?
=(0,0,1),? =(-1,1,m),
=(-1,1,m), =-1,1,0),?
=-1,1,0),? •
• =0,
=0, •
• =0知,
=0知, 為平面BB1D1D的一個法向量.?
為平面BB1D1D的一個法向量.?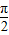 -θ)=
-θ)= =
=
 =
= ,?
,? ,??
,?? 時,直線AP與平面BDD1B1所成角的正切值為3
時,直線AP與平面BDD1B1所成角的正切值為3 .
.

科目:高中數學 來源: 題型:
 如圖,在棱長都相等的正三棱柱ABC-A1B1C1中,D,E分別為AA1,B1C的中點.
如圖,在棱長都相等的正三棱柱ABC-A1B1C1中,D,E分別為AA1,B1C的中點.查看答案和解析>>
科目:高中數學 來源: 題型:

查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在棱長都相等的正三棱柱ABC-A1B1C1中,D,E分別為AA1,B1C的中點.
如圖,在棱長都相等的正三棱柱ABC-A1B1C1中,D,E分別為AA1,B1C的中點.查看答案和解析>>
科目:高中數學 來源:2009-2010學年江蘇省南京市金陵中學高三(上)8月月考數學試卷(解析版) 題型:解答題

查看答案和解析>>
科目:高中數學 來源:2012年安徽省合肥八中高考數學一模試卷(理科)(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com